Спин электрона. Часть 4 – Матрицы Паули.
Первая статья серии про спин тут.
В предыдущей статье мы показали, что каждому направлению спина в квантовой механике соответствует тот или иной вектор состояния. Откуда же берутся численные значения векторов состояния для направлений тех или иных осей? Оказывается, что
любой измеряемой величине в квантовой механике соответствует матрица,
в том числе и спину. Причем,
после измерения система описывается одним из собственных векторов матрицы измеряемой величины.
Что такое собственный вектор проще всего понять на примере обычных векторов. Матрица в этом случае выражает какое-либо действие с векторами (поворот, масштабирование, сдвиг и т.п.). Умножая матрицу на вектор получаем другой вектор (повернутый, увеличенный в размере). Например, следующая матрица масштабирует (увеличивает в 3 раза) в направлении диагонали x=y.
\(\displaystyle\begin{pmatrix}
2 & 1\\
1 & 2
\end{pmatrix}
\binom{x}{y} = \binom{x’}{y’}\)
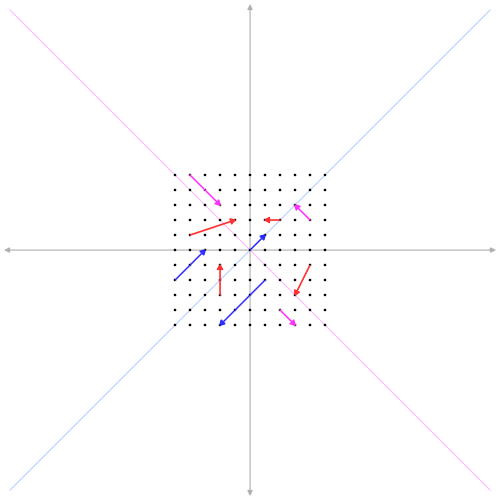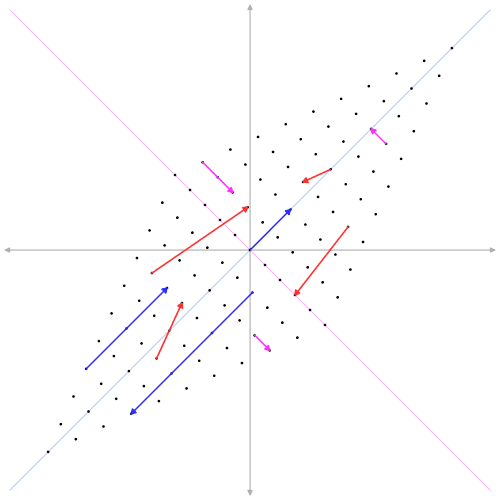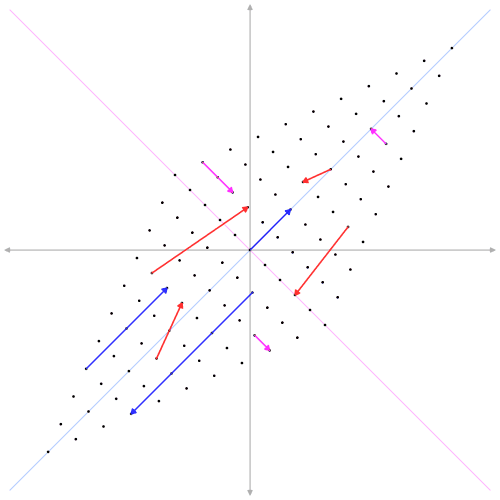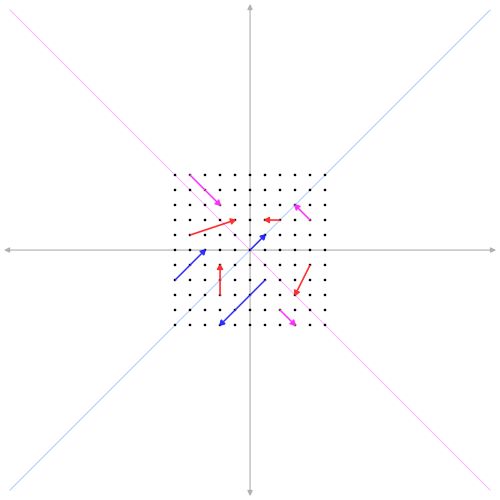
Собственные векторы матрицы – это те что не меняют направление при воздействии данной матрицы. Синие и розовые на анимации – это собственные векторы данного преобразования (матрицы). Собственные векторы идут в паре с собственными значениями. Собственное значение – это просто число, обозначающее во сколько раз изменилась длина собственного вектора при преобразовании. У розовых в нашем случае собственное значение равно единице (длина не изменилась), а у синих 3 (увеличилась в три раза). Математически все сказанное можно сформулировать так: если вектор \(\displaystyle \boldsymbol{v} \) это собственный вектор матрицы M, то умножение матрицы на этот вектор сводится к умножению на число \(\displaystyle \lambda \) (собственное значение):
\(\displaystyle \hat{M}\boldsymbol{v}=\lambda \boldsymbol{v} \) если \(\displaystyle \boldsymbol{v} \) — собственный вектор
Итак, спиновая матрица Паули оси z выглядит как:
\(\displaystyle\hat{\sigma _{z}}=\begin{pmatrix}
1 & 0\\
0 & -1
\end{pmatrix}\)
Ее собственные векторы это вектор состояния электрона со спином вверх (собственное значение +1):
\( \displaystyle|\uparrow\rangle = \binom{1}{0}\)и вниз (собственное значение -1):
\( \displaystyle|\downarrow\rangle = \binom{0}{1}\)Проверьте, что при умножении матрицы на эти векторы мы получим те же самые, умноженные на собственное значение. Собственные значения в квантовой механике играют особую роль .
Собственные значения – это те значения, которые могут получится при измерении величины, описываемой данной матрицей.
В случае спиновых матриц это +1 или -1, соответствующих измеренному спину «вверх» и «вниз». Это математическое описание эффекта квантования: мы не можем получить при измерении спин каким-либо другим, поскольку других собственных значений у данной матрицы нет. Та же самая причина, например, кроется в дискретности энергетических уровней в атомах: энергия – это измеряемая величина и, соответственно, тоже описывается матрицей.
Две другие матрицы спина относительно осей y и x имеют вид:
\(\displaystyle
\hat{\sigma _{y}}=\begin{pmatrix}
0 & -i\\
i &0
\end{pmatrix}\);
\hat{\sigma _{x}}=\begin{pmatrix}
0 & 1\\
1 &0
\end{pmatrix}\)
Их собственные значения также +1 и -1, а собственные векторы мы уже приводили.
Заметили симметрию матриц? Это не случайно. Измеряемым величинам соответствуют только эрмитовы матрицы. Их собственные значения и диагональные элементы – это действительные числа, а остальные элементы симметричны относительно диагонали и являются комплексно-сопряженными друг другу.
Теперь мы даже можем посчитать вероятность измерения того или иного значения спина электрона относительно любой оси, а не только взаимно перпендикулярных x, y и z. Также как обычный вектор \( \displaystyle v\) можно разложить по трем базисным с соответствующими координатами \( \displaystyle v_{x},v_{y},v_{z}\), матрицу измерения спина относительно любой оси можно составить из матриц Паули:
\(\displaystyle
\hat{\sigma}\cdot \boldsymbol{v}=v_{x}\begin{pmatrix}
0 & 1\\
1 &0
\end{pmatrix}+v_{y}\begin{pmatrix}
0 & -i\\
i &0
\end{pmatrix}+v_{z}\begin{pmatrix}
1 & 0\\
0 &-1
\end{pmatrix}\)
где \(\displaystyle v_{x}, v_{y},v_{z}\) – координаты обычного вектора \(\displaystyle v\), указывающего направление оси (просто числа).
Давайте, например, найдем вероятность того, что электрон со спином «вверх» относительно оси y окажется со спином «вверх» относительно повернутой на 45° оси в плоскости x—y.
Электрон со спином «вверх» относительно оси y описывается собственным вектором матрицы \(\displaystyle \hat{\sigma _{y}} \) с собственным значением +1. Мы его приводили раньше:
|\rightarrow\rangle = \frac{1}{\sqrt{2}}\binom{-i}{1}\)
Вектор, повернутый на 45° это, например, вектор (обычный) с координатами \(\displaystyle (1, 1, 0)\) или \(\displaystyle (1/\sqrt{2}, 1/\sqrt{2}, 0)\) если привести его длину к единице. Матрица, соответствующая измерению спина относительно этой оси равна:
\(\displaystyle\frac{1}{\sqrt{2}}\begin{pmatrix}
0 & 1\\
1 &0
\end{pmatrix}+ \frac{1}{\sqrt{2}}\begin{pmatrix}
0 & -i\\
i &0
\end{pmatrix}=\frac{1}{\sqrt{2}}\begin{pmatrix}
0 & 1-i\\
1+i &0
\end{pmatrix}\)
Ее собственный вектор с собственным значением +1 это:
\(\displaystyle|\nearrow\rangle = \binom{0.5-0.5i}{\sqrt{2}}\)
Для нахождения вероятности необходимо возвести в квадрат абсолютное значение амплитуды вероятности:
\(p=|\langle\nearrow|\rightarrow\rangle |^{2}\approx 0.8536\)Интуитивно можно было бы предположить, что если при угле 0° отклоняется 100% электронов, а при угле 90° отклоняется 50%, то при угле 45° должно отклонится 75%=100-50/2. Интуиция предпочитает линейную аппроксимацию. Правильный результат: 85.36%. И он совпадает с аналитическим выражением:
\(\displaystyle p=\frac{1+cos(\alpha)}{2}\approx 0.8536\) при \(\displaystyle \alpha=\frac{\pi }{4}\)
Видите, откуда-то из матриц косинус вдруг появился. Так классическая механика следует из квантовой.
В квантовой механике также широко распространено употребление понятия оператор. Оператор — это абстрактный математический объект, который в конкретном численном выражении может быть представлен матрицей (в том числе бесконечномерной). Как и вектор, который через координаты может быть по-разному записан в зависимости от базиса или системы координат, один и тот же оператор может быть выражен разными матрицами. Операторы часто обозначают шапочкой наверху как мы сделали выше для операторов спина \(\displaystyle \hat{\sigma}\) (сигма. греческая s. spin.). А иногда вообще ничем не выделяют – операторы в квантовой механике чаще используются чем обычные переменные, поэтому по умолчанию любая буква – это оператор.
Важным взаимным свойством двух операторов является коммутируемость. Известно, что порядок умножения матриц имеет значение. Так вот, если \(\displaystyle \hat{A}\hat{B}=\hat{B}\hat{A}\) говорят, что операторы коммутируют (коммутатор равен нулю). Проверьте, что для любых пар операторов \(\displaystyle\hat{\sigma _{z}},\hat{\sigma _{y}},\hat{\sigma _{x}}\) это не так. Они не коммутируют. В квантовой механике этому есть физическая интерпретация:
величины, операторы которых не коммутируют, нельзя измерить одновременно.
Нельзя одновременно измерить спин относительно двух осей. В случае операторов координаты и импульса данный факт больше известен как принцип неопределенности Гейзенберга.
Следующая статья про принцип суперпозиции.


По-моему, тут ошибка в найденном собственном векторе, который повернут на 45 градусов
Собственные векторы не уникальны. Мой вектор тоже является собственным. Проверьте))
Скажите, пожалуйста, почему Вы говорите, что матрица в примере масштабирует в 2 раза, а не в 3 ? Ведь умножение данной матрицы на вектор х=1 у=1 даёт вектор х’=3 y’=3. К тому же, если просто приложить линейку к экрану, то видно, что длина синих векторов изменяется в 3 раза, а не в 2
Дейстаительно в 3. Опечатка, поправил. Спасибо!
Очень интересные примеры, такие в учебниках редко встретишь (спин вдоль y, по диагонали, а что так можно было? смайлик). Обычно всякой фигней забивают содержание (при группы, изопространства). Больше таких примеров!!!
Интересно, а верно ли будет, представить спиновое пространство как 4-е измерение?
Действительно непонятно в каком пространстве действует спин.
Получается матрица спина допустим на ось y — есть проекция на эту ось.