Относительность 11 — Горизонт событий
Многие ошибочно полагают, что в рамках специальной теории относительности нельзя рассматривать движения с ускорением. Но как мы сейчас увидим, это не так.
Рассмотрим диаграмму Минковского – плоскость t-x. Траектория света на такой диаграмме всегда наклонена под углом 45°. Мировая линия инерциальной системы отсчета, то есть системы движущейся с постоянной скоростью, всегда наклонена под меньшим углом.
Пусть неподвижный наблюдатель в нулевой момент времени находится в точке с координатой x. Если наблюдатель вообще не движется, то его координата x с течением времени не меняется и траектория выглядит просто как вертикальная линия.
Но никто не запрещает нарисовать на диаграмме Минковского также и мировую линию наблюдателя, движущегося с ускорением. При ускоренном движении скорость всегда возрастает, но она не может превысить скорость света. То есть траектория будет ассимптотически приближаться к мировой линии светового луча.
Можно показать, что траектория наблюдателя, движущегося с постоянным ускорением является гиперболой. В матрице преобразований Лоренца мы видели гиперболические синусы и косинусы. t2-x2=const это уравнение гиперболы. Ускоренное движение можно получить последовательным увеличением скорости – последовательным применением преобразований Лоренца. А Лоренцевы преобразования как мы видели отражают гиперболический поворот. То есть поворачиваемая точка в пространстве-времени в отличие от обычного поворота точки на плоскости будет двигаться не по кругу, а по гиперболе.
Бытует ошибочное мнение, что горизонты событий возникают только в общей теории относительности: горизонт событий черной дыры или космологический горизонт событий. Но даже в нашем простом примере ускоренного движения наблюдателя в рамках СТО также возникает горизонт событий.
Пусть у нас имеется 2 наблюдателя. Изначально они находятся в одной точке, скажем x. Один остается неподвижным и его траектория – это вертикальная линия, а другой начинает ускоряться и его мировой линией является гипербола. Пусть неподвижный наблюдатель через фиксированный интервал времени посылает световой сигнал вслед ускоряющемуся. Свет это всегда линии под углом 45.
Но смотрите что происходит. Как только мировая линия неподвижного наблюдателя пересечет линию х=t свет, испущенный им уже никогда не достигнет ускоренного наблюдателя. Для наших двух наблюдателей линия x=t является горизонтом событий. Наблюдатель, пересекший горизонт событий уже не может послать сигнал наблюдателю, находящемуся снаружи горизонта.
Кстати обратное неверно. Ускоряющийся наблюдатель может послать сигнал наблюдателю за горизонт событий. Но он достигнет его когда тот будет уже за горизонтом событий, и он не сможет послать ответ ускоряющемуся наблюдателю. Горизонт событий получается работает как однонаправленный шлюз. Его можно пересечь, но после этого ни сам наблюдатель ни даже свет не могут пересечь его обратно.
Заметьте также, что горизонт событий это просто особенность геометрии пространства Минковского. Некая условная линия в пространстве-времени. С точки зрения теории относительности при пересечении наблюдателем горизонта событий для него самого ничего не происходит. В нашем случае наблюдатель вообще все время находится в одной и той же точке х, он ничего не делает и никак не замечает, что он пересек горизонт событий. Никаких физических явлений при пересечении не происходит. Никакими локальными измерениями он не может определить, что пересек горизонт.
Это просто точка невозврата, он больше не сможет никогда догнать второго наблюдателя если вдруг захочет и даже не сможет послать ему сообщение. Они никогда больше не встретятся, если второй продолжит ускоряться. Но в то же время он как продолжал видеть ускоряющегося наблюдателя, так и продолжает. Свет от ускоряющегося наблюдателя может проникать за горизонт событий.
Давайте теперь посмотрим что происходит с точки зрения ускоряющегося наблюдателя. Пусть он смотрит на неподвижного наблюдателя. Проведем мировые линии световых лучей. С его точки зрения неподвижный наблюдатель никогда не пересечет горизонт событий. Он будет к нему ассимптотически приближаться, его время будет замедляться, но он никогда не пересечет горизонт событий.
Кажется возникает парадоксальная ситуация: неподвижный наблюдатель спокойно проходит за горизонт событий и ничего при этом не замечает, а ускоряющийся видит, что он никогда его не пересечет.
Но это не парадокс, а всего лишь особенности геометрии пространства Минковского. Поскольку принцип эквивалентности Эйнштейна о котором мы скоро поговорим утверждает, что ускоренное движение неотличимо от гравитации, все сказанное про горизонт событий справедливо и для горизонта событий черной дыры.

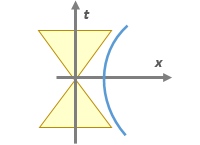

Про горизонт событий ускоряющегося наблюдателя. Да, его скорость не может превысить 1с. И именно поэтому его мировая линия может пересечь линию света на приведенной диаграмме Минковского. Поясните, почему вы только так рисуете, как нарисовали. И почему изображение неподвижного человека не исчезнет, а застрянет для ускоряющегося?