Роль наблюдателя. Базисные векторы и выбор базиса.
Наиболее общим вектором состояния, описывающим квантовомеханическую систему является суперпозиция базисных векторов. Так для спина электрона это вектор:
\( \displaystyle |\psi\rangle= c_{\uparrow}|\uparrow\rangle+c_{\downarrow} |\downarrow\rangle\)Известно, что один и тот же вектор можно выразить через различные базисные векторы.
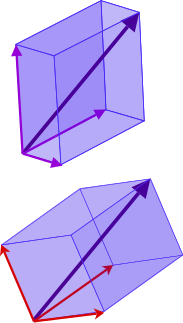
Квантовомеханический вектор состояния также можно выразить через другие базисные векторы, например:
\( \displaystyle |\psi\rangle= c_{\rightarrow}|\rightarrow\rangle+c_{\leftarrow} |\leftarrow\rangle\)Сами базисные векторы можно выразить через базисные векторы другого базиса:
\( \displaystyle
|\rightarrow\rangle= \frac{1}{\sqrt{2}}(-i|\uparrow\rangle+ |\downarrow\rangle)\);
|\leftarrow\rangle= \frac{1}{\sqrt{2}}(-i|\uparrow\rangle- |\downarrow\rangle)\)
Проверить корректность можно через непосредственные матричные вычисления:
\(\displaystyle
\frac{1}{\sqrt{2}}\binom{-i}{1}=\frac{1}{\sqrt{2}}\left [-i\binom{1}{0}+\binom{0}{1}\right ]\);
\frac{1}{\sqrt{2}}\binom{-i}{-1}=\frac{1}{\sqrt{2}}\left [-i\binom{1}{0}-\binom{0}{1}\right ]\)
Представленные базисные векторы являются собственными векторами спиновых операторов
\(\displaystyle\hat{\sigma _{z}},\hat{\sigma _{y}}\), то есть соответствующих матриц Паули. Это общий вывод:
Собственные векторы эрмитовых операторов формируют базис.
Вспомним три правила квантовой механики:
- Эрмитовым операторам (матрицам) соответствуют измеряемые величины.
- При измерении вектор состояния переходит в один из базисных векторов оператора измеряемой величины.
- Если операторы (матрицы) не коммутируют, то соответствующие им физические величины нельзя измерить одновременно.
Получается все базисы изначально равноправны, но наблюдатель делая выбор измеряемой величины одновременно выбирает и базис, формируемый собственными векторами соответствующего оператора. Таким образом, вектор состояния в котором окажется система после измерения определяется:
- Выбором Наблюдателем измеряемой величины (базисных векторов).
- Выбором Природой одного из этих базисных векторов.
Причем квантовая механика позволяет найти вероятность коллапса вектора состояния в тот или иной базисный вектор (второй пункт), но ничего не может сказать о том какой набор базисных векторов выберет наблюдатель (первый пункт).
Пусть наблюдатель захотел измерить спин электрона относительно оси y. При измерении вектор состояния окажется в одном из собственных векторов оператора \(\displaystyle\hat{\sigma _{y}}\), скажем \(\displaystyle |\rightarrow\rangle\). Данный вектор можно представить и в базисе собственных векторов \(\displaystyle\hat{\sigma _{x}}\), как показано выше. Но, если бы он изначально захотел вместо оси y измерить спин относительно оси x, он бы никогда не получил суперпозицию \( \displaystyle \frac{1}{\sqrt{2}}(-i|\uparrow\rangle+ |\downarrow\rangle)=|\rightarrow\rangle\). Возможные варианты это лишь \( \displaystyle |\uparrow\rangle\) и \( \displaystyle |\downarrow\rangle\).
Совершаемый наблюдателем выбор приводит при измерении к результату, который не мог бы получиться никогда, выбери он другой базис. Таким образом базис — величина не влияющая на классические векторы, оказывает самое непосредственное влияние на векторы состояния. Опять же загадочный процесс измерения играет здесь ключевую роль.
Подобные вещи вездесущи в квантовой механике. Можно взять два некоммутирующих эрмитовых оператора и получить полную аналогию описанной ситуации со спином: координата и импульс являются ярким примером.