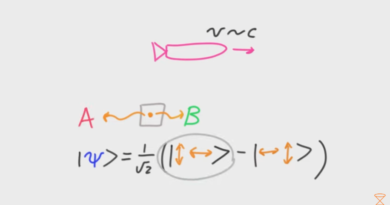Теорема Белла. Часть 2 — Квантовомеханический случай.
В первой части мы показали, что следуя классической логике теории множеств для любых высказываний всегда выполняется неравенство Белла:
\(N(A,\bar{B})+N(B,\bar{C})\geqslant N(A,\bar{C}) \)Оказывается оно может не выполнятся для высказываний, касающихся квантовомеханических объектов. Продемонстрируем данный факт на конкретном примере.
Пусть имеется пара электронов в синглетном состоянии их спинов.
\( \displaystyle |S\rangle=\frac{1}{\sqrt{2}}(|\uparrow\downarrow\rangle-|\downarrow\uparrow\rangle)\)Наши высказывания будут следующими:
\(A \): спин первого электрона направлен вверх по оси z.
\(B \): спин первого электрона направлен по оси, 45º к оси z.
\(C \): спин первого электрона направлен по оси, 90º к оси z.
Отрицания этих высказываний предполагают, что спин первого электрона направлен в противоположное направление относительно этих осей. Но поскольку благодаря свойству синглетного состояния второй электрон антикоррелирован с первым, то выражение «спин первого электрона направлен вниз» эквивалентно выражению «спин второго электрона направлен вверх». Отрицаниями приведенных высказываний будут:
\(\bar{A} \): спин второго электрона направлен вверх по оси z.
\(\bar{B} \): спин второго электрона направлен по оси, 45º к оси z.
\(\bar{C} \): спин второго электрона направлен по оси, 90º к оси z.
Из соображений симметрии \(N(A,\bar{B})=N(B,\bar{C}) \), поскольку в соответствии с нашим выбором высказываний оси, относительно которых измеряется спин, в обоих случаях находятся под углом 45º друг относительно друга. В нашем случае это приводит к упрощению неравенства Белла:
\(2N(A,\bar{B})\geqslant N(A,\bar{C}) \)Остается лишь перевести его на математический язык квантовой механики и проверить справедливость. Для выделения подпространств векторного пространства, соответствующих нашим высказываниям определим соответствующие проекторы:
\(\displaystyle
\hat{p_{A}}=\frac{1}{2}(\hat{\sigma_{z}} +\hat{I}) \);
\(\displaystyle
\hat{p_{\bar{B}}}=(\frac{\hat{\sigma_{x}} +\hat{\sigma_{z}}}{\sqrt{2}} +\hat{I})/2 \);
\(\displaystyle
\hat{p_{\bar{C}}}=\frac{1}{2}(\hat{\sigma_{x}} +\hat{I}) \)
Данные операторы состоят из спиновых матриц 2х2 и действуют на один из спинов. Нам же необходимо действовать на два электрона системы в синглетном состоянии, то есть получить матрицы 4х4. Для этого умножим проекторы тензорно на единичную матрицу — порядок умножения определяет на какой их электронов будет действовать оператор:
\(\displaystyle
\hat{P_{A}}=\hat{p_{A}}\otimes\hat{I}\);
\(\displaystyle
\hat{P_{\bar{B}}}=\hat{I}\otimes\hat{p_{\bar{B}}}\);
\hat{P_{\bar{C}}}=\hat{I}\otimes\hat{p_{\bar{C}}}\)
Таким образом, неравенство Белла на языке квантовой механики запишется как:
\(2\langle S|\hat{P_{A}}\hat{P_{\bar{B}}} |S \rangle \geqslant \langle S|\hat{P_{A}}\hat{P_{\bar{C}}} |S \rangle\)Если произвести все матричные умножения, получим:
\(2\langle S|\hat{P_{A}}\hat{P_{\bar{B}}} |S \rangle =0,1464\);
\(\langle S|\hat{P_{A}}\hat{P_{\bar{C}}} |S \rangle =0,25\)Теорема Белла нарушается! Это не означает, что квантовая механика неверна. Как раз наоборот. Неверна классическая логика в которой неявно предполагается возможность одновременного измерения любых свойств системы без влияния на нее. То есть постулируется объективное существование характеристик объекта безотносительно к наблюдателю и процессу измерения.