Относительность 5 — Пространство Минковского. 4-векторы.

В единицах измерения где скорость света равна единице, его траектория описывается уравнением x=t. Если луч распространяется в сторону отрицательных х, то выражение будет -x=t. Оба их можно скомбинировать записав x²=t² или t²— x²=0. Поскольку скорость света одинакова во всех СО, то данное выражение справедливо во всех СО. То есть в штрихованной СО    t’²— x’²=0. Или t²— x²= t’²— x’².

Преобразования Галилея, связывающие штрихованные и нештрихованные координаты несовместимы с данным равенством. Можно чисто математически найти преобразования, связывающие x и x’, t и t’ и не нарушающие данное выражение. Они как раз окажутся преобразованиями Лоренца. Это еще один из способов их вывода из первых принципов.

Аналогичное выражение для всех трех координат x, y, z будет следующим. Это легко видеть поскольку волновой фронт от вспышки света во всех СО выглядит как сфера. Ее радиус можно найти из декартовых координат по теореме Пифагора и он также равен ct, расстоянию пройденному светом. Или просто t в используемых нами единицах. Возведя обе части равенства в квадрат как раз получим наше выражение t²-x²-y²-z²=0.

Математик Герман Минковский заметил, что оно напоминает формулу нахождения квадрата длины вектора как скалярное произведение вектора с самим собой, записанное через декартовы координаты. Квадрат длины обычного вектора есть сумма квадратов его координат. Это опять же из теоремы Пифагора следует.

Разница с нашим выражением для света лишь в знаках у слагаемых x,y,z и добавлении четвертого слагаемого с t.  Можно умножить обе части равенства на -1 и получить знак плюс перед x,y,z, но слагаемое с временем все равно будет отличаться от пространственных координат противоположным знаком. Также немного необычно, что выражение для света всегда дает ноль даже при ненулевых координатах.

Несмотря на это Минковский предложил мыслить время как 4-ю координату в дополнение к трем пространственным, а сами 4 числа t,x,y,z как координаты точки в четырехмерном пространстве-времени. Можно провести вектор из начала координат в эту точку. Векторы в пространстве Минковского называются 4-векторами. Правда общепринято время не четвертой координатой записывать, а первой, но называть ее не первой, а нулевой.

 Итак, время — это нулевая координата (или компонента) 4-вектора. x,y,z это 1,2,3 компоненты. Такой вектор описывает точку в пространстве-времени, которую еще называют событием.

Формула скалярного произведения таких векторов, дающая квадрат длины, как мы видим немного модифицируется, но в остальном эти 4-векторы ведут себя как обычные векторы.

Такой геометрический подход к теории относительности оказался очень плодотворным. Длина 4-вектора также называется пространственновременным интервалом. Также как длина обычного вектора не меняется при переходе к другой системе координат, длина 4-вектора не меняется при преобразованиях Лоренца. В этом свете переход к другой СО выглядит просто как смена системы координат. Сами 4-векторы не изменяются, меняются лишь координаты t,x,y,z. Все наблюдатели согласятся по поводу длины пространственновременного интервала, хотя координаты t,x,y,z разные в разных СО. Мы поговорим об этом детально в следующих видео.

Из-за наличия знаков минус в формуле вычисления квадрата длины вектора в пространстве Минковского, он может оказаться нулевым при ненулевых координатах или даже отрицательным.

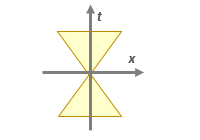
И действительно, как мы видели, для света величина t²-x²-y²-z² всегда равна нулю. Пространственновременной интервал в этом случае соединяет начало координат с точкой на световом конусе. Как мы говорили во второй части, такие интервалы называются светоподобными. Длина светоподобных интервалов всегда нулевая даже при ненулевых координатах 4-вектора. Заметьте, что в обычном евклидовом пространстве такое невозможно. Нулевая длина в случае обычных векторов может получиться только если все координаты нулевые. Это не так в пространстве Минковского, как раз из-за наличия знаков минус в формуле вычисления длины.

Для времениподобного интервала, соединяющего начало координат с точкой внутри светового конуса квадрат длины s² будет больше нуля. Для пространственноподобного интервала, соединяющего начало координат с точкой снаружи светового конуса, квадрат длины s² будет отрицательным. Из-за таких вот особенностей пространство Минковского кардинально отличается от четырехмерного евклидового пространства. В евклидовом пространстве любых размерностей длина вектора неотрицательна. А нулевой длине соответствует только нулевой вектор с нулевыми координатами.

Мы можем соединить интервалом любые 2 точки четырехмерного пространства-времени. По аналогии с евклидовым пространством такой вектор равен разности двух векторов, исходящих из начала координат. В координатной записи квадрат длины такого интервала (Δs)² равен следующему выражению. Он является инвариантом относительно преобразований Лоренца. Во всех СО наблюдатели согласятся по поводу величины квадрата длины. Несмотря на то, что отдельные координаты t,x,y,z разные в разных СО.