Геометрическая интерпретация специальной теории относительности. Световой конус.

Все эффекты специальной теории относительности (замедление времени, сокращение расстояния) можно вывести из преобразований Лоренца, связывающих координаты и время движущейся (штрихованной) и неподвижной систем отсчета:

\( \displaystyle x’= \frac{x-vt}{\sqrt{1-v^2/c^2}}\);

\( \displaystyle t’= \frac{t-(v/c^2) x}{\sqrt{1-v^2/c^2}}\);
Если построить траекторию светового луча на графике где по оси х будет координата, а по оси y время (умноженное на скорость света), то получим линию под углом 45°. Это легко видеть, поскольку для света \( \displaystyle x = сt\).

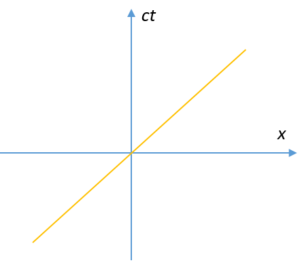
Скорость света в релятивистской физике (relativity — относительность) обычно принимают равной единице (с=1) и расстояние становится эквивалентом времени (световой год, световая секунда и т.п.). Скорость света можно рассматривать как масштабный множитель между единицей времени и единицей расстояния. Вообще-то само определение единицы расстояния (метра) в 1983 г. было подогнано так, чтобы скорость света была ровно 299 792 458 м/с.

Герман Минковский (один из учителей Эйнштейна в Цюрихе) сделал интересное наблюдение. Выражение \( \displaystyle x = сt\)  можно возвести в квадрат и переписать как:

\( \displaystyle s^2= (сt)^2-x^2=0\);
Или для всех трех координат в обозначениях где с = 1:

\( \displaystyle s^2= t^2-(x^2+y^2+z^2)=0\)
Скорость света одинакова во всех системах отсчета, поэтому при преобразованиях Лоренца к штрихованным координатам величина \( \displaystyle s^2\) все равно будет равна нулю. Это можно проверить и непосредственной подстановкой. Минковский провел аналогию с длиной \( \displaystyle l\)  вектора \( \displaystyle a\) , определяемой через его декартовы координаты посредством скалярного произведения с самим собой:

\( \displaystyle a \cdot a=l^2= x^2+y^2+z^2\)
Скалярное произведение векторов \( \displaystyle a= (x_{1}, y_{1}, z_{1})\) и \( \displaystyle b= (x_{2}, y_{2}, z_{2})\) можно записать в более математически изящном виде как:
\( \displaystyle a \cdot b= x_{1} x_{2}+y_{1}y_{2}+z_{1}z_{2}=\sum_{i,j=1}^{3}\delta_{ij} x^i x^j \)

где \( \displaystyle \delta=\begin{pmatrix}
1 & 0 &0 \\
0 & 1 &0 \\
0 & 0 &1
\end{pmatrix} \) это единичная матрица или метрика Евклида,

а через верхний индекс \( \displaystyle x^i \) обозначены декартовы координаты вектора:
\( \displaystyle x^1=x\) ;
\( \displaystyle x^2=y\) ;
\( \displaystyle x^3=z\) ;

Скалярное произведение вектора с самим собой и есть квадрат длины этого вектора. Введение единичной матрицы (которая ничего не делает) изначально может показаться излишним. Но величину \( \displaystyle s^2 \), являющуюся аналогом квадрата длины, также можно записать через скалярное произведение с использованием метрики:

\( \displaystyle s^2=\sum_{i,j=0}^{3}\eta_{ij} x^i x^j \);

где \( \displaystyle \eta=\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & -1 & 0 & 0\\
0 & 0 & -1 & 0\\
0 & 0 & 0 & -1
\end{pmatrix} \) это метрика Минковского,

а координат вектора уже четыре:
\( \displaystyle x^0=t\) ;
\( \displaystyle x^1=x\) ;
\( \displaystyle x^2=y\) ;
\( \displaystyle x^3=z\)

Метрика (от слова мерить) определяет все свойства пространства. Видно, что она входит в определение скалярного произведения и таким образом ответственна как минимум за длины интервалов в пространстве. Метрика Минковского отличается от евклидовой метрики, поэтому пространство Минковского отличается от привычного нам Евклидового пространства. Пространство Минковского является четырехмерным (добавляется время) и часто называется просто пространство-время. Все векторы в нем имеют четыре координаты — время и три пространственные координаты. Не считая знака минус пространство и время входят в метрику симметричным образом. Это очень странно с точки зрения повседневной интуиции поскольку следуя обыденной логике время и пространство ничего общего между собой не имеют. Все кардинальные отличия привычной геометрии Евклида от странной геометрии  пространства-времени Минковского происходят из-за знаков минус в метрике при вычислении скалярного произведения!

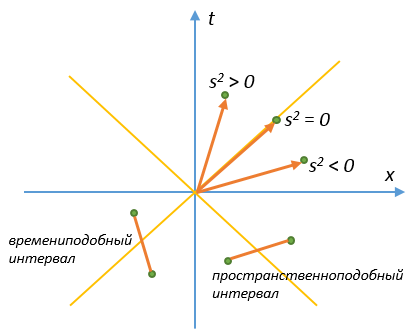
Так квадрат длины 4-вектора (пространственно-временного интервала) в отличие от обычного вектора может быть равен нулю при ненулевом векторе или вообще иметь отрицательную величину:

\( \displaystyle s^2=0\). Это рассмотренный нами случай для светового луча. Светоподобный интервал.

\( \displaystyle s^2>0\). Времениподобный интервал. Временная координата больше пространственной.

\( \displaystyle s^2<0\). Пространственноподобный интервал. Пространственная координата больше временной.

На рисунке показан одномерный случай. В двумерном случае получается конус. Для трехмерного пространства нарисовать не получится, поэтому в картинках ограничиваются двумерным световым конусом.

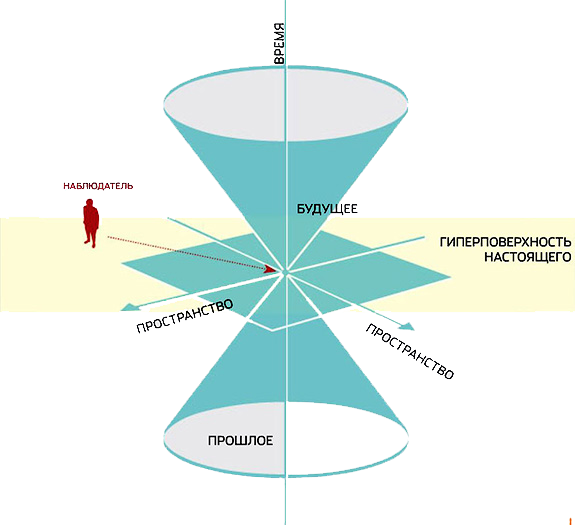
Если считать наблюдателя расположенным в начале координат, то все события, находящиеся в нижнем конусе, доступны ему для наблюдения. Свет и движущиеся с меньшей скоростью объекты  могли достичь начала координат на картинке. То есть точки пространства-времени конуса прошлого могли повлиять на наблюдателя в начале координат.

Верхний конус (конус будущего) — совокупность точек куда физически может переместиться наблюдатель (или свет) в будущем или же просто оказать влияния на события в них.

Световой конус является наглядным отображением причинно-следственной связи. Если два события в пространстве-времени могут быть связаны причинно-следственной связью, то 4-расстояние между ними (его квадрат) времениподобно \( \displaystyle s^2\geqslant 0\). Если два события не связаны причинно-следственной связью, то пространственноподобно \( \displaystyle s^2\leqslant 0\).

Достижение светом задней и передней частей ракеты в мысленном эксперименте с ракетой может служить примером событий, разделенных пространственноподобным интервалом. В этом случае разные наблюдатели могут видеть по-разному очередность наступления событий. Одно не является причиной или следствием другого. В случае событий, разделенных времениподобным интервалом это не так. Например, вспышка лампы в центре ракеты и достижение светом ее конца является таким примером. То есть:

Никакой наблюдатель не может увидеть следствие события перед его причиной, но очередность событий, разделенных времениподобным интервалом может меняться при смене системы отсчета. 

Важно, что пространственно-временной интервал s ведет себя аналогично обычному пространственному интервалу в Евклидовой геометрии в том плане, что он не меняется при смене систем координат. Координаты могут меняться, но длина вектора — физическая величина, она не меняется.

В пространстве Минковского преобразования Лоренца являются преобразованиями по смене системы координат и не влияют на пространственно-временной интервал (длину 4-вектора).  

Но сами координаты (включая время) 4-вектора события в пространстве-времени, конечно зависят от скорости наблюдателя:

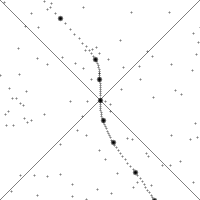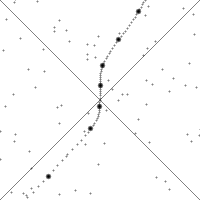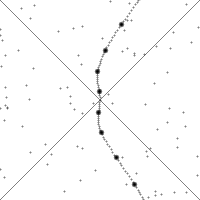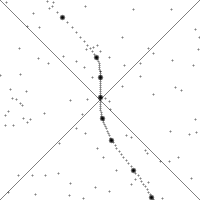
Заметьте, траектория наблюдателя (его мировая линия) никогда не искривляется больше 45°. Это геометрическое отображение факта невозможности движения быстрее скорости света. Пространственные и временные интервалы меняются при изменении скорости наблюдателя (см. про световые часы), но определенный выше интервал \( \displaystyle s^2\) не изменяется. Он инвариантен относительно преобразований Лоренца.

В анимации может показаться, что со временем что-то меняется. На самом деле там пытались показать влияние скорости движения и ускорения наблюдателя на наблюдаемую им картину. Пространство Минковского статично. Время уже включено как одна из координат. С точки зрения геометрии теории относительности, мировая линия (скажем человека) уже существует в пространстве Минковского в виде какой-то кривой, начинающейся от события рождения (точки в пространстве-времени) и заканчивающейся событием смерти (другая точка пространства Минкавского). Прошлое и будущее определены однозначно и не меняются.

Кстати,  в определении метрики Минковского есть неоднозначность. Можно определить интервал и как:
\( \displaystyle s^2= x^2-(сt)^2\)
и получить противоположные знаки в матрице и в определении времениподобных и пространственноподобных интервалов. К сожалению устоявшейся терминологии так и нет, половина литературы использует одни обозначения, а вторая половина — другие.