Группа Лоренца
Координаты (t‘, x‘) движущейся в положительном направлении оси x со скоростью v системы связаны с координатами (x, t) неподвижной системы отсчета преобразованиями Лоренца:
\( \displaystyle x’= \frac{x-vt}{\sqrt{1-v^2/c^2}}\);
\( \displaystyle t’= \frac{t-(v/c^2) x}{\sqrt{1-v^2/c^2}}\)При выражении нештрихованных координат через штрихованные меняется только знак при скорости (кто относительно кого движется). В натуральных единицах измерения, где скорость света принята равной единице, такие преобразования имеют вид:
\( \displaystyle x = \frac{x’+vt’}{\sqrt{1-v^2}}\);
\( \displaystyle t = \frac{t’+v x’}{\sqrt{1-v^2}}\)Их можно записать в матричном виде:
\( \displaystyle \frac{1}{\sqrt{1-v^2}} \begin{pmatrix}1&v \\
v&1
\end{pmatrix} \binom{t’}{x’} =\binom{t}{x} \)
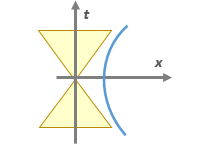
Геометрия играет большую роль в выработке интуиции и понимании теории относительности. Геометрический смысл становится более понятным если переписать преобразования через тригонометрические функции:
\( \displaystyle \begin{pmatrix}
cosh(\beta)&sinh(\beta) \\
sinh(\beta)&cosh(\beta)
\end{pmatrix} \binom{t’}{x’} =\binom{t}{x} \), где \( \displaystyle \beta=atanh(v)\)
Они крайне непохожи, но это действительно та же самая матрица преобразований Лоренца, записанная в более изощренном виде. Не случайно траектория наблюдателя, движущегося с постоянным ускорением, является гиперболой. В матрице преобразований оказывается стоят гиперболические синусы и косинусы.
Матрица имеет полную аналогию с матрицей поворота точки на плоскости на угол \( \displaystyle \alpha\):
\( \displaystyle \begin{pmatrix}cos(\alpha) &-sin(\alpha) \\
sin(\alpha)&cos(\alpha)
\end{pmatrix} \binom{x’}{y’} =\binom{x}{y} \)
Таким образом, преобразования Лоренца — своего рода поворот системы координат на угол \( \displaystyle \beta\) в пространстве Минковского. Понятно, что угол связан со скоростью (пусть даже и через гиперболический арктангенс)).
Операции поворота образуют группу. Поворот можно осуществить на любой угол, поэтому элементов группы бесконечно много, но все они параметризованы углом. Такие группы называются группами Ли. Они обладают интересным свойством — элемент группы получается экспоненцированием параметра (угла поворота), умноженного на так называемый генератор.
Звучит сложнее, чем выглядит. В случае матрицы поворота на плоскости:
\( \displaystyle \begin{pmatrix}cos(\alpha) &-sin(\alpha) \\
sin(\alpha)&cos(\alpha)
\end{pmatrix} = e^{\alpha \begin{pmatrix}
0 &-1 \\
1&0
\end{pmatrix}}\)
Аналогично для гиперболического поворота:
\( \displaystyle \begin{pmatrix}cosh(\beta ) &sinh(\beta ) \\
sinh(\beta )&cosh(\beta )
\end{pmatrix}= e^{\beta \begin{pmatrix}
0 &1 \\
1&0
\end{pmatrix}}\)
Матрицы с единицами как раз и являются генераторами поворотов.
Группы математически выражают интуитивное понятие симметрии. При применении симметричного преобразования какая-то величина должна остаться неизменной, инвариантной относительно этих преобразований. В нашем случае не изменяется пространственно-временной интервал \( \displaystyle ds^2=dt^2-dx^2-dy^2-dz^2\). Группа Лоренца как раз и включает в себя преобразования, оставляющие неизменным этот интервал: преобразования Лоренца (гиперболические повороты) и обычные повороты в трехмерном евклидовом пространстве.
Матрицы генераторов проще матриц преобразований, но они несут в себе ту же информацию, поэтому с ними удобнее работать. Таким образом у нас имеются три генератора преобразований, соответствующие движению вдоль осей x, y и z:
\( \displaystyle K_{1}=\left ( \begin{array}{c|ccc}0 & 1 & 0 & 0\\ \hline
1 & 0 & 0 & 0\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0
\end{array}\right )\) \( \displaystyle K_{2}=\left ( \begin{array}{c|ccc}
0 & 0 & 1 & 0\\ \hline
0 & 0 & 0 & 0\\
1 & 0 & 0 & 0\\
0 & 0 & 0 & 0
\end{array}\right )\) \( \displaystyle K_{3}=\left ( \begin{array}{c|ccc}
0 & 0 & 0 & 1\\ \hline
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0\\
1 & 0 & 0 & 0
\end{array}\right )\)
И три генератора обычных поворотов вокруг осей x, y и z:
\( \displaystyle L_{1}=\left ( \begin{array}{c|ccc}0 & 0 & 0 & 0\\ \hline
0 & 0 & -1 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 0
\end{array}\right )\) \( \displaystyle L_{2}=\left ( \begin{array}{c|ccc}
0 & 0 & 0 & 0\\ \hline
0 & 0 & 0 & 1\\
0 & 0 & 0 & 0\\
0 & -1 & 0 & 0
\end{array}\right )\) \( \displaystyle L_{3}=\left ( \begin{array}{c|ccc}
0 & 0 & 0 & 0\\ \hline
0 & 0 & 0 & 0\\
0 & 0 & 0 & -1\\
0 & 0 & 1 & 0
\end{array}\right )\)
За счет того, что в метрику четырехмерного пространства Минковского время входит с противоположным знаком, чем три пространственные координаты, симметриями затрагивающими время (первые строка и столбец в матрицах генераторов) являются гиперболические повороты. Остальной кусок матрицы — матрица 3х3 в правом нижнем углу отражает обычные повороты в привычном нам трехмерном пространстве. Именно поэтому геренаторы и разбиваются на такие две подгруппы. Гениальная идея Минковского сделать равноправными пространственные и временную координаты из-за знака минус имеет свои ограничения и на деле мы видим четкое деление.
Если возвести матрицы генераторов в экспоненту, получим матрицы преобразований (элементы группы Лоренца), которые можно комбинировать и умножать на 4-векторы. Они будут приводить к изменениям координат векторов (время и пространство), но оставлять без изменения инвариант — длину этого 4-вектора, называемого также собственной длиной, собственным временем или просто интервалом.
Преобразования группы Лоренца оставляют нетронутым начало координат (ведь это вращения). Если учитывать еще и смещения (трансляции) всей системы координат, которые сдвигают ноль, но тоже оставляют нетронутым длину 4-вектора, то получим группу Пуанкаре. Свойствами этих групп по-сути и исчерпываются все свойства пространства-времени специальной теории относительности.