Световые часы: замедление времени, сокращение расстояния.
Принцип относительности приводит к неизменности скорости света вне зависимости от направления или скорости движения самой системы. Но скорость это отношение расстояния ко времени. Если не меняется скорость, значит меняются расстояния и время. Наглядно данный факт демонстрируют световые часы.
Луч света движется между двумя зеркалами. За единицу времени можно принять время прохождения луча между зеркалами. В неподвижной системе отсчета пройденное светом расстояние это просто \( \displaystyle L=c\Delta t_{0}\) — расстояние между зеркалами.

В движущейся системе координат луч идет по гипотенузе, а L можно найти через теорему Пифагора:
\( \displaystyle L=\sqrt{(c\Delta t)^{2}-(v\Delta t)^{2}}=c\Delta t\sqrt{1-v^2/c^2}\)При низких скоростях релятивистский множитель с корнем приближается к единице и релятивистские поправки (relativity-относительность) становятся ничтожно малы.
Таким образом наш интервал времени в движущейся системе координат равен:
\( \displaystyle \Delta t=\frac{L}{c} \frac{1}{\sqrt{1-v^2/c^2}}\)Подставляя \( \displaystyle c\Delta t_{0}\) вместо L получим связь интервалов времени разных систем отсчета:
\( \displaystyle \Delta t=\Delta t_{0} \frac{1}{\sqrt{1-v^2/c^2}}\)Интервал времени \( \Delta t\) в движущейся системе координат более длинный. За одну секунду в движущейся системе пройдет более одной секунды в неподвижной. То есть время в движущейся системе отсчета замедляется.
Cкорость света (отношение расстояния ко времени) одинакова во всех системах координат, а время, как мы выяснили, течет по-разному. Поэтому при замедлении времени, расстояние должно сокращаться на тот же самый множитель, чтобы скорость света не изменилась.
Это можно продемонстрировать перевернув на 90 градусов световые часы, чтобы луч шел параллельно направлению движения.
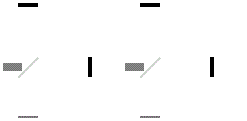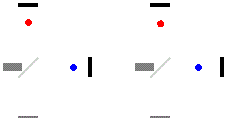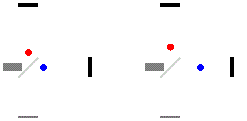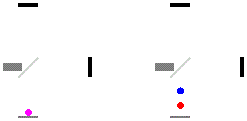
По пути к зеркалу луч проходит расстояние L плюс то расстояние, на которое успело сдвинуться зеркало.
\( \displaystyle c\Delta t_{1}=L+v\Delta t_{1}\);
\( \displaystyle \Delta t_{1}=\frac{L}{c-v}\);
По пути обратно луч проходит расстояние L минус то расстояние, на которое успело приблизиться первое зеркало.
\( \displaystyle c\Delta t_{2}=L-v\Delta t_{2}\);
\( \displaystyle \Delta t_{2}=\frac{L}{c+v}\);
Общее время равно их сумме:
\( \displaystyle \Delta t=\frac{L}{c+v}+\frac{L}{c-v}=\) \( \displaystyle \frac{2L}{c}\cdot\frac{1}{1-v^2/c^2}\)Сравнивая с предыдущим случаем для вертикально расположенных часов мы видим, что выражения различны. Горизонтальные и вертикальные часы идут по-разному. Устранить это можно только предположив, что само расстояние между зеркалами сократилось: \( \displaystyle L\rightarrow L \sqrt{1-v^2/c^2}\).
В общем случае все расстояния по направлению движения сокращаются:
\( \displaystyle \Delta x=\Delta x_{0} \sqrt{1-v^2/c^2}\)

А вот интересно, позади движущейся на субсветовой скорости ИСО пространство тоже сжимается? По идее да но тогда парадокс — мы улетаем дальше от точки а она как бы ближе становится тиа догоняет. И потом должен быть какой горизонт событий сзади чтобы не нарушалась причинно-следственная связь.
И вообще получается что теоретически можно додететь до любой галактики. С точки зрения неподвижного наблюдателя на корабле уменьшается время и он может по неподвижным часам лететь милионы лет. А для тех кто на борту сжимается пространство и им лететь как бы намного ближе.
Очень хорошая статья! Всё объяснено понятно. Но возникают 2 вопроса:
1. Зачем здесь видео, демонстрирующее «несимметричность» замедления времени? Ведь согласно СТО все системы равноправны, и которая «движется» мы не знаем. Видео некорректно.
2. В анимации с горизонтальными и вертикальными часами нужно подразумевать, что левая картинка — с точки зрения ИСО, связанной с часами, а правая — с неподвижным наблюдателем. Тогда в правой не учтено то, что «красный свет» движется по наклонной (с т. зрения неподв. наблюдателя) => синий и красный всё равно придут одновременно. Нет сокращения расстояния, есть сокращение длины, это совсем другой эффект.
Второе утверждение не верно!
1. Красный идет медленнее, чем на картинке слева (учтено движение по наклонной),
2. Сокращение расстояний есть! Это сравнимо с сокращением длины. Здесь вот в чем дело: неподвижному наблюдателю кажется, что у подвижного
1. замедляется время и
2. сокращается длина,
а вот для подвижного:
1. сокращается расстояние,
2. кажется, что время замедляется у неподвижного (т.к. ситуация симметрична).
Это очень коротко, просто и понятно описано здесь: http://phscs.ru/physicsus/distance-reduce На примере достижения мюонами поверхности Земли.
В случае с гор. и верт. часами именно замедление времени и сокращение расстояния (длины часов) объясняют то, что часы идут синхронно. В статье об этом правильно!
да, мультик с часами левый, наверно двоешник рисовал
Все согласны с этим издевательством? Луч это волна. У волны всегда скорость одна — скорость распространения волны в среде. Угол 90 градусов означает — путь вверх и путь вниз полностью совпали в среде. И это же означает — нет бокового смещения света даже если параллельные зеркала имеют перпендикулярную скорость. Итого — наблюдение траектории движения луча со стороны не имеет никакого отношения к его поведению в среде. Зачем весь этот бред? Картинка с права вообще описывает сверх световое движение, не может горизонтальный катет быть длиннее вертикального! Тогда длина гипотенузы даже при адекватном катете, меньшем скорости света есть мнимой величиной величиной, просто растянутой проекцией вертикального катета за время вертикального катета. Ничего ровным счётом не изменилось. Если же луч изначально повернуть под углом, то будет по прежнему косая дистанция до параллельных зеркал которая опять ни как не изменяется поскольку свет снова волна и скорость его по прежнему равна скорости света и не какие зеркала ничего не меняют пока по прежнему движение их не вызывает эффекта погони и встречи в пространстве луча и зеркала. Для этого направление смещения зеркал должно измениться на 90 градусов, а часы называться не поперечными, а продольными. Извините. Но чем вы думаете когда вам демонстрируют этот бред?