Спин электрона. Часть 3 – Вектор состояния и амплитуда вероятности.

Первая часть по спин здесь.

На предыдущих примерах один и два мы выяснили, что спин ведет себя довольно странно и может описываться классическим вектором (направленным отрезком) лишь после его измерения. До момента измерения предположение о существовании такого вектора приводит к логическим противоречиям.

Однако квантовомеханические системы все-таки описываются некоторым абстрактным обобщением вектора, называемым вектор состояния. Вектор состояния уже нельзя представить себе направленным отрезком, однако если записывать его через координаты, то математика формально совпадает с известной для обычного вектора.

Перейдем к конкретным вычислениям для наглядности. Вектор состояния электрона со спином «вверх» относительно произвольной оси (скажем оси z) выглядит как:

\(\displaystyle \binom{1}{0}\)

Числа 0 и 1 в вектор-столбце условно можно сравнить с координатами обычного вектора. Если бы это был вектор с декартовыми координатами (x, y), то можно было бы интерпретировать данную запись как вектор единичной длины, указывающий в положительном направлении оси x. То есть интерпретировать компоненты  вектора как декартовы координаты:

\(\displaystyle \binom{a_{x}}{a_{y}}\)

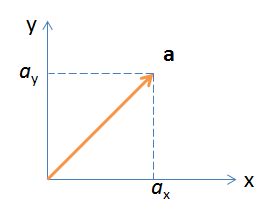
Но этого не следует делать для вектора состояния! Математика та же, но наглядность в случае векторов состояния пропадает. Любая геометрическая аналогия приводит к недоразумениям. Доверять приходится только математике. Вектор состояния электрона со спином вниз относительно той же оси z выглядит как:

\(\displaystyle \binom{0}{1}\)

Опять же, для обычного вектора с координатами (x, y) это можно было бы интерпретировать как вектор в направлении оси y (перпендикулярной оси x). На самом деле данный вектор состояния описывает спин «вниз», то есть не перпендикулярный, а повернутый на 180° относительно «вверх».

Квантовая механика представляет собой набор принципов. Вот один из самых главных:

Вероятность осуществления того или иного события равна квадрату абсолютного значения скалярного произведения конечного и исходного векторов состояния.

Звучит непонятно! Поясним. Предположим электрон пройдя прибор Штерна-Герлаха отклонился вверх. Мы хотим, например, узнать вероятность того что он также отклонится вверх если его затем пропустить через второй точно такой же прибор. Следуя правилу, надо вычислить скалярное произведение соответствующих векторов и возвести его в квадрат. Скалярное произведение обычных векторов можно найти через произведение их длин на косинус угла между ними. Но у векторов состояния нет углов (о попытках геометрической интерпретации надо забыть!), поэтому применяют альтернативную формулу, использующую только координаты векторов: скалярное произведение равно сумме произведений соответствующих координат (кстати это справедливо и для обычных векторов). Для корректной записи первый вектор-столбец необходимо превратить в вектор-строку чтобы использовать формулу матричного произведения (строка на столбец):

\(\displaystyle \left |
\begin{pmatrix}
1 & 0
\end{pmatrix}
\binom{1}{0}
\right |^{2}=
\left |
1\cdot 1+0\cdot 0
\right |^{2}=1\)

Результатом является единица (100%). То есть все электроны, отклонившиеся вверх в первом приборе отклонятся вверх и во втором. Точно так же можно, например, посчитать вероятность того, что электрон отклонившийся вниз в первом приборе отклонится вверх во втором:

\(\displaystyle \left |
\begin{pmatrix}
1 & 0
\end{pmatrix}
\binom{0}{1}
\right |^{2}=
\left |
1\cdot 0+0\cdot 1
\right |^{2}=0\)

Заметьте: исходное состояние справа, конечное – слева. Вероятность равна нулю, что и следовало ожидать. Мы говорили, что электрон сам по себе спин не меняет. Если он направлен вниз, то он точно не направлен вверх. Когда скалярное произведение векторов состояния равно нулю, говорят, что они ортогональны (для обычных векторов это случай когда они перпендикулярны).

Что же насчет двух других взаимно перпендикулярных осей y и x? Вектор состояния спина электрона, направленного вверх относительно оси y («вправо» фактически) выглядит как:

\(\displaystyle \binom{-i/\sqrt{2}}{1/\sqrt{2}}\)

Вот это уже странно и не так интуитивно. Во-первых все две координаты вектора отличны от нуля. Во вторых, в первой координате присутствует мнимая единица. Действительно, в общем случае координаты вектора состояния это комплексные числа и это еще одна причина почему его нельзя представить направленным отрезком. В случае векторов состояния даже не используют термин «координаты», а говорят «компоненты». В дальнейшем мы тоже будем следовать данной общепринятой терминологии. Вектор состояния спина электрона, направленного вниз относительно оси y («влево» фактически) выглядит как:

\(\displaystyle \binom{-i/\sqrt{2}}{-1/\sqrt{2}}\)

Используя данные векторы состояний можно на количественном уровне пройтись по всем экспериментам, описанным в первой и второй частях.

Например, какова вероятность того, что электрон отклонится влево во втором приборе Штерна-Герлаха, если он отклонился вниз в первом (повернутом на 90°). Или если по-другому сформулировать: какова вероятность что спин при измерении окажется «влево», если сейчас он «вниз»? Надо посчитать скалярное произведение и возвести в квадрат:

\(\displaystyle \left |
\frac{1}{\sqrt{2}}
\begin{pmatrix}
i & -1
\end{pmatrix}
\binom{0}{1}
\right |^{2}=
\left |
\frac{-1}{\sqrt{2}}
\right |^{2}=
\frac{1}{2}\)

Получаем 0.5, то есть вероятность 50%. Вы заметили, что при переводе вектор-столбца в вектор-строку мы поменяли знак при мнимой единице? Это не опечатка. В случае векторов состояния помимо замен столбцов на строки (транспонирование) необходимо также менять знак при мнимой единице на противоположный (комплексное сопряжение). Комбинация этих двух операций  называется эрмитово сопряжение.

Ну и относительно третьей оси x вектор состояния вверх (от нас) выглядет как:

\(\displaystyle \binom{1/\sqrt{2}}{1/\sqrt{2}}\)

а «спин вниз» (к нам):

\(\displaystyle \binom{-1/\sqrt{2}}{1/\sqrt{2}}\)

Убедитесь сами, что их скалярное произведение равно нулю. Скалярное произведение вектора с самим собой равно единице, а с векторами всех других перпендикулярных осей 0.5 (после возведения в квадрат).

Как и в математике обычных векторов, у квантовомеханических векторов состояния устоялась абстрактная запись не привязанная к координатам (компонентам). Вектор-столбец (кет-вектор) обозначается правой скобкой

\( |\psi\rangle\)

а вектор-строка (бра-вектор) левой:

\(\langle\psi|\)

Скалярное произведение вместо точки обозначается просто расположенными рядом бра- и кет- скобками (бра-кет=bracket=скобка) и называется в квантовой механике — амплитуда вероятности. Видимо по аналогии с амплитудой электрического поля световой волны и ее квадратом — интенсивностью (количеством фотонов). Обозначения введены одним из отцов-основателей квантовой механики Дираком. Амплитуда вероятности (скалярное произведение) векторов \(\psi\) и \(\phi\) обозначается так:

\(\langle\psi|\varphi \rangle\)

Амплитуда вероятности это просто число (в общем случае комплексное). При возведении в квадрат абсолютного значения амплитуды вероятности мы получаем саму вероятность.

Буквы внутри этих скобок не несут никакой информации кроме как сказать нам о каком векторе мы говорим. Например, можно переписать выше представленные матричные вычисления в этом абстрактном, но более компактном виде:

 \(|\langle\uparrow|\uparrow \rangle |^{2}=1\)

 \(|\langle\uparrow|\downarrow\rangle |^{2}=0\)

 \(|\langle\leftarrow|\downarrow\rangle |^{2}=\frac{1}{2}\)

В следующей статье продолжим знакомство с математическим аппаратом квантовой механики.