Теорема Белла. Часть 1 — Классический случай.

Теорема Белла формулируется в рамках классической математической логики (теории множеств).  Большую популярность она приобрела благодаря тому, что наглядно демонстрирует несостоятельность этой казалось бы нерушимой логики в случае применения теоремы к квантовомеханическим объектам.

Напомним как логические операции «И», «ИЛИ» и «НЕ» выглядят на языке теории множеств. Операция ИЛИ это объединение множеств. Если точками условно показать логические высказывания, а овалами — множества высказываний, то те высказывания которые входят или в множество А или в множество В как раз и формируют объединенное множество А ИЛИ В.

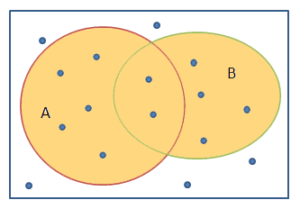
Операция И  — это пересечение множеств. Высказывания входящие в множество А и в то же время входящие в множество В находятся в их пересечении: А И В.

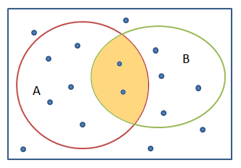
Операция НЕ — это инверсия, отрицание. Высказывания не входящие в множество А формируют множество НЕ А, показанное на рисунке.

Неравенство Белла, справедливость которого доказывается теоремой Белла выглядит так:

\(N(A,\bar{B})+N(B,\bar{C})\geqslant N(A,\bar{C}) \)

где \(N(A,\bar{B})\) — количество высказываний, входящих в А, но не входящих в В; \(N(B,\bar{C}) \) — количество высказываний, входящих в В, но не входящих в С; \(N(A,\bar{C}) \) — количество высказываний, входящих в А, но не входящих в С.

Доказательство становится очевидным если каждое из членов неравенства представить графически:

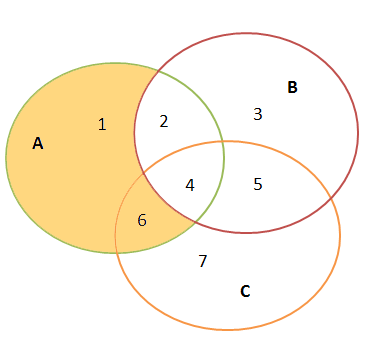
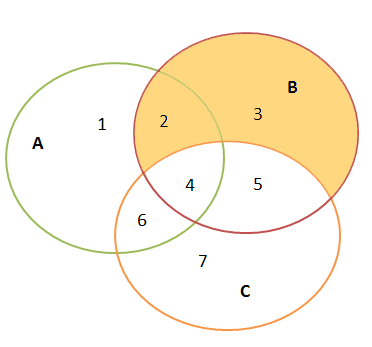
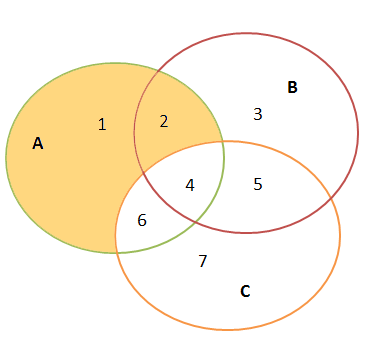
Из графических соображений видно, что неравенство верно при любых расположениях множеств А, В, С. Если обозначить через N1….N7 количества высказываний в каждой из возможных пронумерованных на рисунках подобластей, то можно увидеть данный факт даже алгебраически, переписав неравенство в виде:

\((N1+N6)+(N2+N3)\geqslant (N1+N2) \)

Логика кажется железной и наглядной. Неравенство простое и всегда верное. Кажется по-другому и не может быть. Действительно теорема верна в рамках классической логики, то есть применительно к высказываниям, касающимся макроскопических объектов нашей повседневной жизни. Поэтому ее верность так «интуитивна». Но оно может нарушаться если высказывания будут относиться к квантовомеханическим объектам. В Части 2 мы продемонстрируем пример такого нарушения.

Если неравенство нарушается, значит неверны какие-то из исходных предположений. В случае квантового мира неверны сами основы классической логики: возможность вести рассуждения о свойствах и логических отношениях различных объектов, как будто они объективно существуют. То есть в классической логике не учитывается роль наблюдателя и неявно предполагается объективное существование свойств объектов, которые к тому же все можно узнать одновременно.