Спин электрона. Часть 7 — Операторы проекции (проекторы).

Мы уже встречались с проекцией когда говорили про амплитуду вероятности в Части 3 про спин. Скалярное произведение двух векторов не что иное как проекция одного вектора да другой. Именно поэтому амплитуда вероятности равна нулю для ортогональных векторов состояния и единице при скалярном произведении вектора с самим собой.

Но проецировать можно не только на вектор. Обычный трехмерный вектор можно проецировать на плоскость, например x-y:

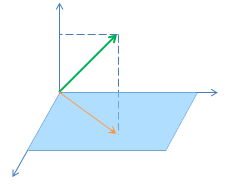
В общем случае N-размерного вектора его можно проецировать на любое из подпространств размерности N-1, N-2 и т.д.

Все операции с векторами можно представить как действие оператора. Проекции вектора на подпространство тоже соответствует оператор. Так в случае на картинке этот оператор обнуляет z-координату вектора:

\(\displaystyle
\hat{P}\boldsymbol{v}=\begin{pmatrix}
1 & 0 & 0\\
0 & 1 &0\\
0 & 0 &0\\
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
z \\
\end{pmatrix}=
\begin{pmatrix}
x \\
y \\
0 \\
\end{pmatrix}
\)

В квантовой механике с помощью операторов проекции можно составлять логические высказывания относительно квантовомеханических систем и  и вычислять вероятности их истинности или ложности. То есть необходимо составить оператор проекции касательно какого-либо утверждения. Вероятность того, что это утверждение верно для системы в состоянии \(|\psi\rangle\) можно найти вычислив ожидаемое значение соответствующего оператора проекции:

\(\textit{вероятность}=\langle\psi|\hat{P} |\psi\rangle\)

Оператор \(\hat{P} \) действует на кет-вектор \(|\psi\rangle\) в результате чего получается другой кет-вектор, который вместе с бра-вектором \(\langle\psi|\) формируют скалярное произведение. В отличие от амплитуды вероятности данное число будет всегда действительным. Это способ извлекать вероятностные предсказания из математического аппарата квантовой механики, альтернативный описываемому ранее.

Приведем пример. В статье про запутанные состояния мы утверждали, что если пара электронов находится в синглетном состоянии, то при измерении спина одного из электронов относительно любой оси мы получим вероятность 50% спин «вверх» и 50% спин «вниз».

Оператор проекции высказывания «спин направлен по оси n» можно выразить через матрицы Паули:

\(\displaystyle\hat{P}=\frac{ \hat{\sigma} \cdot n+\hat{I}}{2}\)

где  \(\displaystyle \hat{\sigma} \cdot n\) — произведение матриц Паули с компонентами вектора n направления оси (полное выражение здесь).   \(\displaystyle \hat{I}\)  — единичная матрица.

Так матрица оператора проекции высказывания «спин электрона направлен вверх по z» выглядит:

\(\displaystyle
\hat{P_{z}}=\frac{1}{2}(\hat{\sigma_{z}} +\hat{I}) =\begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix}
\)

Проверьте сами используя тензорное произведение базисных векторов \(|\uparrow\rangle\) и \(|\downarrow\rangle\) , что синглетное состояние в матричном представлении имеет вид:

\( \displaystyle |S\rangle=\frac{1}{\sqrt{2}}(|\uparrow\downarrow\rangle-|\downarrow\uparrow\rangle)=\frac{1}{\sqrt{2}}\begin{pmatrix}
0 \\
1 \\
-1 \\
0 \\
\end{pmatrix}\)

Скажем нас интересует спин первого электрона. Тогда для получения оператора проекции в виде матрицы 4х4 для применения к вектору синглетного состояния умножаем тензорно оператор проекции для одного спина на единичную матрицу:

\(\displaystyle
\hat{P_{1,z}}=\hat{P_{z}}\otimes\hat{I}=
\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0
\end{pmatrix}
\)

Вероятность получается 50%:

\(\langle S|\hat{P_{1,z}} |S \rangle=
\frac{1}{2}
\begin{pmatrix}
0 & 1 & -1 & 0
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
0 \\
1 \\
-1 \\
0 \\
\end{pmatrix}
\)=0.5

Убедитесь, что результат 50% получается при любой оси, то есть любого оператора \(\hat{P}\)  определенного выше независимо от координат вектора направления оси n, а также справедлив и для второго электрона.

Таким образом мы доказали одно из основных свойств синглетного запутанного состояния \(|S\rangle\) — спины электронов максимально коррелированы между собой (измеряя первый мы фактически измеряем и второй) и в то же время результат измерения спина относительно любой оси абсолютно случаен. Данная ситуация не имеет классического аналога.