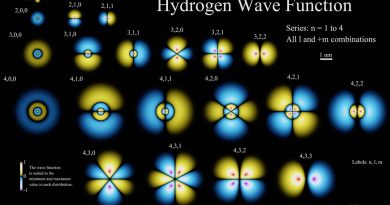
Удивительная история предсказания антиматерии #1

Сегодня об антиматерии знает каждый школьник. Но не всем известно, что ее существование изначально было предсказано теоретически. Экспериментальные подтверждения появились позже. Объединение специальной теории относительности и квантовой механики неизбежно приводит к тому, что для каждой частицы должна существовать частица той же массы, но с противоположным зарядом.

Никто прежде никогда не видел никаких античастиц. К тому же теория говорит, что при встрече частицы с античастицой происходит их аннигиляция с выделением большого количества энергии в соответствии со знаменитой формулой E=mc2. Опять же никто никогда не видел никаких взрывов от столкновений материи с антиматерией. Многие были уверены, что если теория предсказывает никогда не наблюдаемые частицы, то она просто неверна. Однако автор теории, Пол Дирак, придерживался другого принципа. Он написал его на доске в 1956 году будучи с визитом в МГУ: Физические законы должны обладать математической красотой. Эту его надпись с тех пор не стирают с доски. И действительно, теория Дирака чрезвычайно красива с математической точки зрения. Давайте перенесемся в начало XX века.

В 1905 году Эйнштейн перевернул мир своей теорией относительности. Вот что Дирак вспоминает о том времени:

…возникла теория относительности, замечательная идея, открывающая дорогу к новому образу мышления. Мне кажется, что ни до ни после ни одна научная мысль, которой удавалось завладеть умами широкой пуб­лики, не производила равного по своей силе эффекта. Этот эффект происходил одновременно и от специальной, и от общей тео­рии относительности. На самом деле, специальная теория относительности восходила к 1905 г. и была значительно старше. Тем не менее, кроме нескольких университетских специалистов о ней никто ничего не знал. Обыватель никогда не слышал об Эйнштейне, и вдруг имя Эйнштейна оказалось у всех на устах. Я тогда учился на инженерном факультете Бристольского университета и, конечно же, был охвачен общим возбуждением, которое породила теория относительности. Мы очень много говорили о ней.

Теория выглядела как задача, доступная всем: обнаружив нерелятивистскую формулу, имеющую какой-­нибудь физический смысл, надо переписать ее так, чтобы она согласовывалось со специальной теорией относительности. Это было очень похоже на игру, и я втягивался в нее при первой же возможности. Время от времени получался интересный для меня результат и я написал по этому поводу небольшую статью.

В 1926 году Вернер Гейзенберг выдвигает новые идеи, которые всего за год развились в теорию, называемую сейчас  квантовой механикой. В том же 1926 году Эрвин Шредингер публикует свое знаменитое уравнение. Однако сразу возникла проблема: уравнение Шредингера не релятивистское. То есть оно не согласуется с теорией относительности Эйнштейна. С самого начала было понятно, что это уравнение является всего лишь приближением. Приближением к некоему пока неизвестному релятивистскому уравнению.

Конечно Шредингер публикуя в 1926 году свое уравнение понимал его ограниченность. Изначально он хотел найти релятивистское уравнение, описывающее как он думал волны материи. И он даже нашел такое. Сейчас оно известно как уравнение Клейна-Гордона. Но он попробовал применить его к атому водорода и результаты противоречили эксперименту. Поэтому он не стал его публиковать и в итоге ограничился нерелятивистским уравнением, которое давало правильный спектр для водорода. Сейчас мы знаем, что уравнение Клейна-Гордона не работает для электронов потому что описывает скалярные поля: пи-мезон, например, или бозон Хиггса. Электрон же, в отличие от них, имеет ненулевой спин.

Надо сказать, что про существование спина было известно еще до формулировки Гейзенбергом и другими отцами-основателями постулатов КМ. Необходимость спина следовала из экспериментов по измерению спектров атомов. Хотя первоначальные идеи объяснения спектров сейчас конечно смотрятся наивными. Вот, например, Вольфганг Паули вспоминает:

То что спектры давали целые числа 2, 8, 18, 32 — длины периодов в системе химических элементов, бурно обсуждалось в Мюнхене, включая замечание шведского физика Ридберга о том, что эти числа имеют простую форму 2n² , где n принимает целочисленные значения. Зоммерфельд особенно старался связать число 8 с количеством углов куба.

В 20-е годы до работы Гейзенберга была популярна модель атома Бора. В ней электроны представлялись шариками, вращающимися вокруг ядра, по аналогии с планетами солнечной системы. Однако было не понятно почему все электроны не располагаются на одной ближней к ядру орбите, как должно происходить с точки зрения принципа минимизации энергии. Паули занялся этой проблемой:

Осенью 1924 года я выдвинул предположение о новом квантово-теоретическом свойстве электрона, которое я назвал «двузначностью, не поддающейся классическому описанию». Изложение общей формулировки принципа запрета было сделано в Гамбурге весной 1925г.

Простыми словами, принцип запрета Паули гласит, что два и более электрона не могут находиться в одном и том же состоянии. Эксперименты однако показывали, что на атомной орбите может находится либо один либо два электрона. Но тогда согласно принципу запрета эти два электрона должны находиться в разных состояниях. Они должны чем-то отличаться. Та самая двузначность, которую затем назвали спином. Два электрона на орбите отличаются спином. Как это часто бывает, принять новые неинтуитивные концепции оказываются в состоянии далеко не все.

За исключением экспертов по классификации спектральных линий, физикам было трудно понять принцип запрета, поскольку в терминах модели не было придано никакого смысла четвертой степени свободы электрона.

Под первыми тремя степенями свободы Паули конечно же имеет в виду координаты x y z.  Спин можно мыслить четверной координатой в абстрактном конфигурационном пространстве, но эта координата не непрерывная, а дискретная и может принимать только одно из двух значений. Ранее такого никогда в физике не встречалось.

Паули также сетует на то, что эту новую степень свободы (спин) приходится вводить в теорию искусственно. Я не смог найти логическую причину существования принципа запрета и вывести его из более общих предположений. Забегая немного вперед скажем, что это удалось Дираку. Его релятивистская теория электрона предсказывает существование спина. Однако Паули сумел обобщить уравнение Шредингера и учесть также и спин. Вот его статья 1927 года где он вводит уравнение, известное сейчас как ур-е Паули, а также свои знаменитые матрицы Паули.

Согласно постулату КМ любой наблюдаемой величине должна соответствовать матрица (оператор). Спин – это наблюдаемая величина. И она  может принимать только два значения.  Тогда спину должна соответствовать матрица 2х2. Поскольку спин связан с вращением, а пространство у нас трехмерно, спиновых матриц также оказывается три. Ключевым нововведением Паули стало то, что эти матрицы появляются как коэффициенты в его уравнении. Ранее никогда в физике не встречались уравнения в которых коэффициенты  являются не числами, а матрицами. Это было кардинально ново. Из-за этого волновая функция в уравнении Паули оказывается двухкомпонентной. Таких двухкомпонентных полей тоже никто никогда прежде не видел.

Сам Шредингер вообще мыслил свою волновую функцию как реальную волну материи. Но в обобщении Паули она оказалась двухкопмонентной. Уравнение Паули, также как и уравнение Шредингера, все же нерелятивистское. Оно не согласуется с теорией относительности Эйнштейна. Конечно же Паули пытался найти релятивистское уравнение, но это не удалось даже такому гению как ему.

… мне до сих пор не удалось прийти к релятивистски инвариантной формулировке квантовой механики электрона, которую можно считать достаточно естественной и непринудительной.

Паули высказывает в статье свое мнение, что для построения релятивистской теории электрона потребуется кардинальный пересмотр существующих понятий. И в ближайшем будущем релятивистское уравнение электрона не будет найдено. В первом  утверждении он оказался прав, но во втором нет. Релятивистское уравнение было получено Полом Дираком уже в следующем (1928) году.