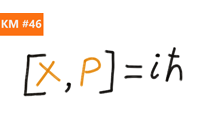Запутанные состояния. Entanglement.
Восемнадцатая часть введения в квантовую механику.
Наконец мы подошли к такому интересному и не имеющему классических аналогов явлению как Entanglement. К сожалению для такого важного понятия в русском языке нет устоявшейся терминологии. Слово Entanglement как только не переводят: квантовая запутанность, запутанные состояния, квантовые корреляции.
Что же такое квантовые запутанные состояния?
Многие столетия наука развивалась по пути редукционизма. То есть исследовались все более и более мелкие составляющие больших систем. Атомизм служит ярким примером. Согласно нему все состоит из атомов, поэтому изучая атомы можно понять поведение состоящих из них макроскопических объектов. Здесь неявно предполагается, что любую систему можно рассматривать как набор независимых составляющих, взаимодействующих друг с другом. Это кажущееся очевидным предположение справедливо в Ньютоновской механике, поэтому оно нам так интуитивно. Нашим мозгом оно воспринимается просто как факт. Хочешь понять как что-то работает – разбери на части и посмотри.
Оказывается в квантовой механике не все так просто.
Давайте для конкретики возьмем простую составную систему из двух спинов электронов. То есть наша система представляет собой два электрона, но нас интересуют только их спины. Пусть спин первого электрона направлен вверх по оси z. В матричной записи он представляется следующим вектором. Пусть спин второго электрона также направлен вверх по z. Вектор состояния комбинированной системы будет описываться тензорным произведением этих векторов. В матричной записи это будет уже вектор–столбец с четырьмя компонентами. То есть такой вектор живет в четырехмерном Гильбертовом пространстве.
Знак тензорного произведения обычно опускают. Чаще данное произведение вообще записывают в виде одного кет-вектора с двумя стрелочками. Первая относится к спину первого электрона, а вторая к спину второго. Остальные три возможности также представляются аналогичными вектор-столбцами. Заметьте, что все четыре вектора ортогональны друг другу. То есть они могут служить базисными векторами четырехмерного Гильбертова пространства.
Наиболее общий вектор состояния спина электрона записывается суперпозицией базисных векторов. a1 и a2 это амплитуды вероятности при измерении спина по оси z обнаружить его в состоянии вверх и вниз. Для спина второго электроны мы имеем аналогичное выражение. Вектор состояния системы из этих двух спинов также записывается тензорным произведением этих векторов. Раскрыв скобки получим четыре слагаемых.
Но данное выражение не является наиболее общим вектором состояния системы из двух спинов. Компоненты наиболее общего вектора состояния не обязаны иметь вид произведения двух комплексных чисел. Они могут быть произвольными комплексными коэффициентами. Ограничением для них является лишь условие нормировки. То есть сумма квадратов абсолютного значения должна равняться единице. Некоторые из этих амплитуд вероятности вообще могут быть равны нулю.
Пусть скажем с1 и с4 равны нулю, с2 равно 1/sqrt_2, а с3 равно -1/ sqrt_2. Тогда вектор состояния будет иметь следующий вид. Он называется синглетным состоянием и является примером запутанного состояния. Entangled State. Он также описывает систему из спинов двух электронов. Но заметьте, что мы не можем более отделить спин первого электрона от спина второго. Более невозможно представить этот вектор в виде двух сомножителей где первый относится только к спину первого электрона, а второй к спину второго. То есть более невозможно рассматривать каждый из спинов независимо. Они связаны или говорят запутаны между собой.
Заметьте, что спин каждого из электронов не определен. При измерении спина любого из двух электронов мы получим спин вверх с вероятностью 50% и спин вниз с вероятностью 50%. Но измерение даже одного из спинов приводит к коллапсу всего вектора состояния. Этот коллапс позволяет нам со 100%-ой уверенностью сказать, что спин второго электрона при измерении относительно той же оси окажется противоположным первому. Можно даже не проводить это второе измерение. Одно единственное наблюдение дает нам информацию сразу о двух спинах.
Мы наблюдаем корреляции. Если спин первого электрона при измерении оказался вверх по оси z, то спин второго будет вниз. Если спин первого оказался вниз, то спин второго точно будет направлен вверх относительно той же оси. Эти корреляции не связаны с каким-либо физическим взаимодействием двух электронов. Электроны со спином в синглетном состоянии можно разнести на разные концы Вселенной, но корреляции будут сохраняться.
Однако их нельзя использовать для передачи информации со сверхсветовой скоростью. Результат измерения единичного спина всегда случаен. Нам ничего не даст информация о том, что спин электрона на другом конце Вселенной при измерении окажется вниз или вверх.
Запутанные состояния схожи с классическими корреляциями. Скажем если я не глядя перемешаю две разноцветные таблетки и зажму в кулаки, то посмотрев и увидев в правой руке красную, я точно знаю, что в левой руке у меня синяя. Однако в квантовом случае сами классические характеристики (цвет таблетки или спин электрона) не определены до момента измерения. Они находятся в квантовой суперпозиции альтернативных возможностей. К тому же мы имеем свободу выбора базиса, то есть свободу выбора самой измеряемой характеристики.
Существование запутанных состояний позволяет строго математически доказать факт отсутствия классических характеристик до момента измерения. Что мы в дальнейшем и сделаем.