Спин электрона. Часть 2 — Электроны в магнитном поле.

Это вторая часть серии про спин электнона.

Часть 1 — Эксперимент Штерна-Герлаха.

Приведем еще один эксперимент наглядно демонстрирующий отличия квантовой механики от классической.

Предположим электроны находятся в сильном постоянном магнитном поле. Спину энергетически более выгодно ориентироваться по направлению поля, поэтому если поле достаточно сильное, то спустя некоторое время можно считать, что в каком бы направлении спины не указывали до включения поля, сейчас они ориентированы по полю. Что будет если резко поменять полярность магнита?

Электроны вдруг окажутся в невыгодном  энергетическом состоянии: возбужденном, по направлению против магнитного поля и следовательно обладающим большей энергией. Поэтому через некоторое время они опять выстроятся вдоль поля, тем самым уменьшив свою энергию, которая уйдет в виде фотона. Можно сказать, что энергия испускаемого фотона равна работе по переводу спина электрона из состояния «вниз» в состояние «вверх» (и наоборот) при данной величине магнитного поля.

Теперь интересно посмотреть что произойдет если повернуть магнит на 90° вместо180°.

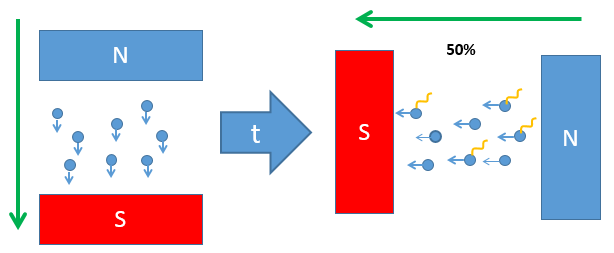
Спустя некоторое время спины выровняться вдоль поля (влево), но фотон излучится только у половины электронов. Причем энергия всех фотонов будет одинакова и равна энергии по переводу из положения «спин вниз» в «спин вверх», то есть той же, что в случае на первой картинке.

Как это интерпретировать? Можно сказать, что у электронов излучивших фотон спин до этого был направлен вправо, а у электронов не излучивших фотон спин уже был направлен влево. Ведь энергия испущенного фотона – это та, которая необходима для поворота спина на 180°. Он не мог быть направлен куда-либо еще кроме «вправо» и «влево» согласно закону сохранения энергии.

Тут надо понимать, что как и в предыдущем случае с приборами Штерна-Герлаха все дело в квантовании. Следуя классической логике, каждый электрон должен был испустить фотон с энергией в два раза меньше, чем на первой картинке. Ведь поворот был не на 180°, а на 90°, соответственно и затрачиваемая на поворот энергия должна быть в два раза меньше. Однако в случае спина электрона, фотон не может быть испущен с произвольной энергией. Возможны только два варианта — либо он испускается с энергией «из вверха вниз» либо не испускается вообще. Предсказать какой именно из электронов излучит фотон также невозможно. Но квантовая механика позволяет посчитать вероятность осуществления данного события.

Опять же нельзя говорить об ориентации спина относительно данной оси до момента измерения за исключением если ось не менялась или менялась на противоположно направленную. Спин относительно конкретно взятой оси в общем случае не определен (не выражается классической величиной) до момента измерения.

Если повернуть магнит обратно в исходное состояние, то опять 50% электронов излучит фотон, но не тех же самых, что излучали при первом повороте. Нет! Опять совершенно случайным образом! То есть измерение спина (получение информации о его ориентации любым способом) относительно оси x делает неактуальной информацию о предыдущем измерении относительно другой оси y.

Что будет если повернуть магнит на произвольный, скажем малый, угол?

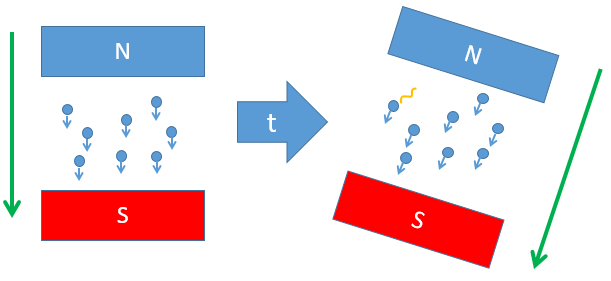
Если повернуть на угол, к примеру 10°, то почти все электроны со спином «вниз» относительно исходной оси окажутся и со спином вниз относительно повернутой. Но небольшая их часть все же излучит фотон. То есть спины этих электронов были направлены «вверх» относительно этой новой оси хотя недавно они были направлены «вниз» относительно почти той же оси (10° разницы!). Определить какие именно электроны испустят фотон опять же невозможно в принципе. Все электроны были в одинаковых условиях и один ничем не отличается от другого. Все элементарные частицы считаются тождественными, то есть невозможно отличить один электрон от другого.

Переход от квантовой к классической физике происходит при рассмотрении большого количества электронов. В этом случае мы получаем то, что интенсивность испускаемого излучения (количество фотонов) плавно меняется от угла поворота. Что и наблюдается в экспериментах. Точную формулу можно вывести из математического аппарата квантовой механики, который мы начнем рассматривать в Части 3 про спин.

Существует видеоверсия этого поста.