Метрика. Метрический тензор.

Метрика (от слова мерить), называемая также метрическим тензором, позволяет находить длины и таким образом несет ответственность за всю геометрию пространства.

Длину \( \displaystyle s\) вектора можно найти через его декартовы координаты по теореме Пифагора:

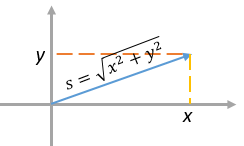
Обычно говорят о квадрате длины, являющейся также скалярным произведением вектора с самим собой:
\( \displaystyle s^{2}=x \cdot x + y \cdot y\)

Поскольку размерность пространства может быть больше двух, координаты удобно различать не буквами, а индексом (верхним):
\( \displaystyle s^{2}=x^{1} \cdot x^{1} + x^{2} \cdot x^{2}\),
что теперь удобно переписать через знак суммы:
\( \displaystyle s^{2}=\sum_{i=1}^{2} x^i x^i \)

Метрика немного обобщает эту формулу для вычисления квадрата длины вектора:
\( \displaystyle s^{2}=\sum_{i,j=1}^{N}g_{ij} x^i x^j \),
где N — размерность пространства; g — метрика.

В нашем простом случае метрика представляется единичной матрицей:

\( \displaystyle g=\begin{pmatrix}
1&0 \\
0& 1
\end{pmatrix}\)

То есть в развернутом виде квадрат длины имеет запись:

\( \displaystyle s^{2}=1\cdot x^{1} x^{1} +0\cdot x^{1} x^{2}+0\cdot x^{2} x^{1}+1\cdot  x^{2} x^{2}\)

Перекрестные члены в скалярном произведении уходят за счет соответствующих нулей в метрике.

Длину кривой можно представить, состоящей из суммы длин бесконечно малых векторов:

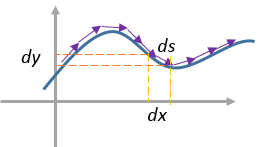
По аналогии с обычными векторами, квадрат длины бесконечно малого вектора:

\( \displaystyle ds^{2}=dx^2 + dy^2 \),

а длина кривой — их сумма (интеграл):

\( \displaystyle s=\int \sqrt {dx^2 + dy^2}\) \( \displaystyle =\int \sqrt {1 + \left (\frac{dy}{dx}\right )^2}dx\)

То есть если кривая задана функцией \( \displaystyle y(x)\), для вычисления ее длины необходимо найти ее производную и вычислить вышеприведенный интеграл.

Формула справедлива в декартовых координатах, где метрика равна единичной матрице. Рассмотрим для примера полярные координаты, где точка на плоскости представляется радиусом и углом, то есть координатами \( \displaystyle (r,\theta )\) :

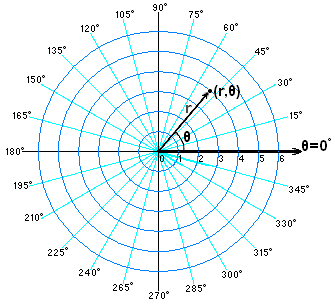
Метрика полярных координат:

\( \displaystyle g=\begin{pmatrix}
1&0 \\
0& r^2
\end{pmatrix}\),

или для квадрата длины:

\( \displaystyle ds^{2}=dr^2 + r^2 d\theta ^2 \),

Наличие множителя \( \displaystyle r^2 \) объясняется увеличением длины дуги фиксированного угла при увеличении радиуса. Если задать кривую в виде функции \( \displaystyle r(\theta) \), то длина кривой будет определятся как:

\( \displaystyle s=\int_{\theta_{1}}^{\theta_{2}} \sqrt {\left (\frac{dr}{d\theta}  \right )^2 + r^2} d\theta\)

Можно, например, использовать данную формулу для нахождения длины окружности. В этом случае \( \displaystyle r\) не зависит от \( \displaystyle \theta\), поэтому \( \displaystyle \frac{dr}{d\theta} =0\):

\( \displaystyle s=\int_{0}^{2\pi} \sqrt {0 + r^2} d\theta=\) \( \displaystyle r\int_{0}^{2\pi}d\theta=2\pi r\)

Не обязательно все элементы метрики кроме диагональных равны нулю. Если перейти от декартовых к криволинейным координатам, например:
\( \displaystyle u=x+2y\);
\( \displaystyle v=x-y\),
то метрика в этих координатах будет выглядеть:

\( \displaystyle g=\begin{pmatrix}
2/9&1/9  \\
1/9& 5/9 \\
\end{pmatrix}\),

Вид метрики зависит не только от системы координат, но и от самого рассматриваемого пространства. В приведенных выше примерах мы оставались в рамках Евклидовой геометрии. Но существуют и другие, где не действуют некоторые факты Евклидовой геометрии, например, о сумме углов треугольника или непересекаемости параллельных линий, но описанный математический аппарат работает везде. Простейший пример искривленного пространства — поверхность сферы.

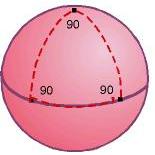
Это двумерное пространство. В координатах, заданных двумя углами вектора из начала координат \( \displaystyle (\theta, \phi)\),  метрика имеет вид:

\( \displaystyle g=\begin{pmatrix}
R^2&0 \\
0& R^2 sin^2 \theta
\end{pmatrix}\),

где R — фиксированный радиус сферы.
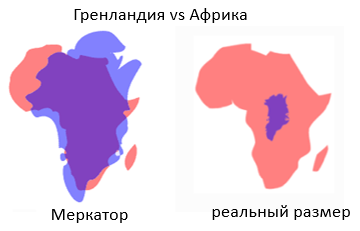
Данную метрику нельзя привести к декартовой метрике плоскости никакими преобразованиями координат. То есть нельзя отобразить поверхность сферы на плоскость без искажений. Например, на карте мира (проекция Меркатора) Гренландия кажется в 2—3 раза больше Австралии и сравнима по размерам с Южной Америкой. В реальности Гренландия втрое меньше Австралии и в 8 раз меньше Южной Америки.

Существуют и более экзотические пространства. Например, пространство Минковского, называемое также пространство-время специальной теории относительности. Это четырехмерное пространство с координатами \( \displaystyle (t, x, y, z)\)  и метрикой Минковского:

\( \displaystyle \eta=\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & -1 & 0 & 0\\
0 & 0 & -1 & 0\\
0 & 0 & 0 & -1
\end{pmatrix} \)

В таком пространстве даже квадрат длины может быть отрицательным. Но оно все равно является плоским. Искривленное пространство-время описывается общей теорией относительности. Так метрика пространства-времени вблизи черной дыры (и любого другого сферически симметричного тела) в координатах \( \displaystyle (t, r, \theta, \phi)\)  получила название метрика Шварцшильда:

\( \displaystyle g=\begin{pmatrix}
\left (1 -r_s/r \right )& 0 & 0 & 0\\
0 & -\left (1 -r_s/r \right )^{-1} & 0 & 0\\
0 & 0 & -r^2 & 0\\
0 & 0 & 0 & -r^2 sin^2 \theta
\end{pmatrix} \),

где

\( \displaystyle r_s=\frac{2GM}{c^2}\) — радиус Шварцшильда, известный как горизонт событий черной дыры.

См. также статью про Манхэттенскую метрику и метрику Чебышева.

Все теперь в телеграм: https://t.me/lightcone_qm