Интеграл и оператор интегрирования
Если дифференциал связан с разностью, то интеграл — с суммой (integrate — совмещать, объединять). Знак интеграла представляет собой вытянутую S (summ — сумма). Интегрирование — операция обратная дифференцированию. Если нам дана функция \( \displaystyle f(x)\), являющаяся производной другой функции \( \displaystyle y(x)\):
\( \displaystyle f(x)=\frac{dy(x)}{dx}\)или
\( \displaystyle dy(x)=f(x)dx\),
то чтобы найти эту функцию (первообразную) достаточно проинтегрировать обе стороны равенства:
\( \displaystyle \int dy(x)=\int f(x)dx\)Поскольку символ интеграла \( \displaystyle \int \) выполняет действие, обратное символу дифференциала \( \displaystyle d \), то в левой части равенства они сокращаются и мы получаем:
\( \displaystyle y(x)=\int f(x)dx\)Интеграл функции \( \displaystyle f(x)\) на отрезке \( \displaystyle [a, b]\) это площадь под кривой, очерченной данной функцией (с минусом в отрицательных значениях).
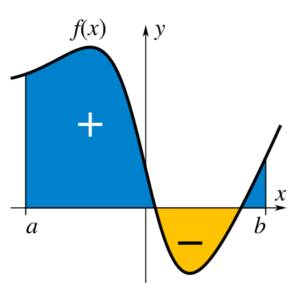
Каждому интервалу \( \displaystyle [a, b]\) соответствует число — значение интеграла для этого интервала. Если сделать длину интервала «плавающей», то совокупность получившихся точек как раз и будет первообразной функцией:
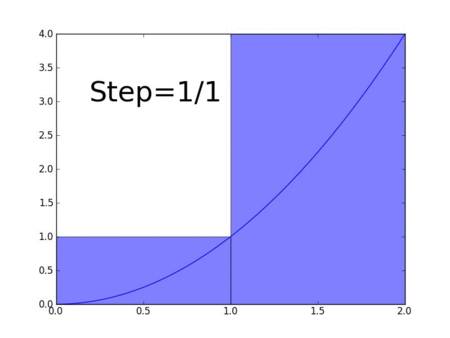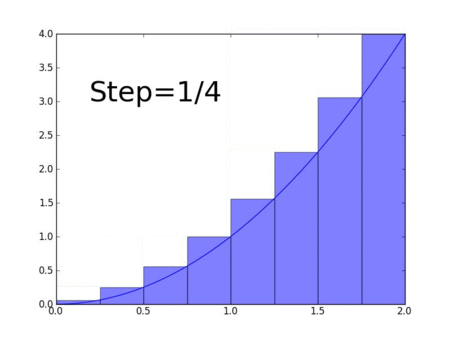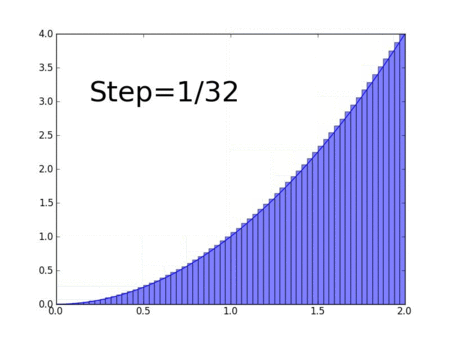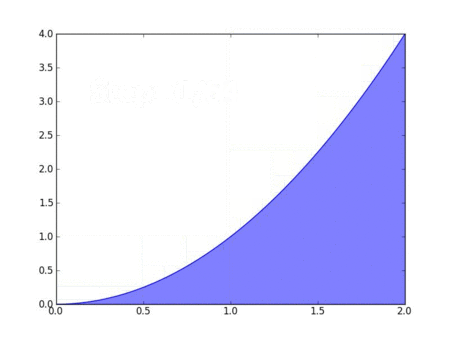
\( \displaystyle y(x)=\int_{a}^{x} f(t)dt\)Операцию интегрирования, по аналогии с дифференцированием, можно представить как действие оператора. Для этого достаточно рассмотреть приближенное вычисление площади под кривой, разбив ее на конечное число точек и суммируя вклад каждого из прямоугольников.
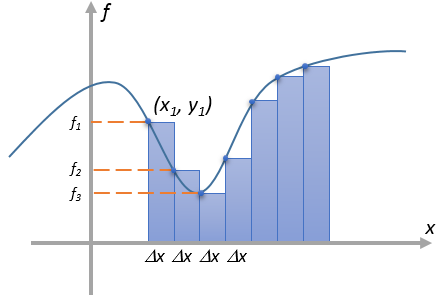
Декартовы y-координаты дискретной функции можно записать в вектор-столбец:
\( \displaystyle f(x)=\begin{pmatrix}f_{1}\\
f_{2}\\
f_{3}\\
…\\
f_{n}
\end{pmatrix}\)
А интегрирование можно записать в виде умножения матриц:
\( \displaystyle \int f(x)dx=\) \( \displaystyle \Delta x\begin{pmatrix}
1&0 &0 &… &0 \\
1&1 &0 &… &0 \\
1&1 &1 &… &0 \\
…&… &… &… &…\\
1& 1& 1& …&1
\end{pmatrix}\begin{pmatrix}
f_{1}\\
f_{2}\\
f_{3}\\
…\\
f_{n}
\end{pmatrix}=\) \( \displaystyle \Delta x\begin{pmatrix}
f_{1}\\
f_{1}+f_{2}\\
f_{1}+f_{2}+f_{3}\\
…\\
f_{1}+…+f_{n}
\end{pmatrix}\)
Произведение квадратной матрицы на вектор-столбец (исходная функция), дает другой вектор-столбец (первообразная функция). То есть получившийся вектор-столбец (умноженный на \( \displaystyle \Delta x\)) как раз будет являться аппроксимацией интеграла исходной функции. Проверьте, что умножая приведенную матрицу по стандартному правилу «строка на столбец» мы получим вектор, состоящий из суммы значений функции в точках, что (умноженное на \( \displaystyle \Delta x\)) и является интегралом, поскольку площадь одного прямоугольника равна произведению значения функции в точке (одна сторона) на \( \displaystyle \Delta x\) (другая сторона). Это еще одна наглядная демонстрация почему интеграл связан с суммой, достаточно посмотреть на вектор-столбец результата.
Заметьте, что мы свели операцию интегрирования к простому умножению матриц. Если вектор-столбец является аппроксимацией функции, то приведенная матрица (умноженная на \( \displaystyle \Delta x\)) — это аппроксимация самого оператора интегрирования.
То есть при \( \displaystyle \Delta x \rightarrow 0\) матрица и вектор-столбец будут бесконечномерными и мы перейдем от аппроксимации к действительным величинам: функциям и операторам над ними. То есть оператор и матрица фактически одно и тоже в нашем контексте. Кстати, матрицами можно представлять и более простые операции.
Одной из точек зрения на процесс интегрирования является взгляд с позиции линейных операторов. Оператор (operator — выполняющий операцию) это то, что действует на функцию в результате чего получается другая функция. По прямой аналогии примера с матрицами алгебраически можно записать:
\( \displaystyle \hat{I}f(t)=\int f(t)dt\)где за \( \displaystyle \hat{I}\) обозначен оператор интегрирования.
Читать следует так: оператор \( \displaystyle \hat{I}\) действует на исходную функцию \( \displaystyle f \) в результате чего получается другая функция. Действие оператора можно представить графически как изменение сигнала неким преобразователем:
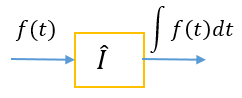
Поскольку операторы интегрирования и дифференцирования обратны друг другу, введение блока интегрирования излишне. Получить первообразную возможно и с помощью блока дифференцирования.
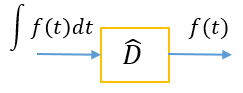
Можно также записать операторные уравнения, например:
\( \displaystyle \hat{I}=\hat{D}^{-1}\);
\( \displaystyle \hat{D}=\hat{I}^{-1}\);
\( \displaystyle \hat{I}\hat{D}=\hat{D}\hat{I}=\hat{1}\),
где за \( \displaystyle \hat{1}\) обозначен «ничего не делающий» оператор тождественности, который аппроксимируется единичной матрицей. За (-1) обозначен обратный оператор или обратная матрица в случае аппроксимации.
Порядок умножения операторов, как и матриц, имеет значение. Существует даже величина, называемая коммутатор, обозначаемая квадратными скобками и определяемая для операторов \( \displaystyle \hat{A}\) и \( \displaystyle \hat{B}\) как:
\( \displaystyle [\hat{A}, \hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A}\).
В случае наших операторов коммутатор \( \displaystyle [\hat{I}, \hat{D}]\) равен нулю — без разницы интегрировать ли сначала, а потом дифференцировать или наоборот. В этом случае говорят, что операторы коммутируют. В общем случае коммутатор двух операторов не равен нулю и порядок действий имеет значение. В квантовой механике этот факт несет глубокий физический смысл.


