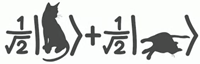Квантовая логика

Нарушение неравенств Белла влечет за собой собой более глубокие последствия, чем на первый взгляд может показаться. В частности, из них следует что сама классическая логика не работает в квантовой механике. Давайте воспользуемся теорией множеств для наглядного изображения логических выражений.

Скажем у нас есть множество А, множество В и множество С. Логическое высказывание может оказаться в множестве А. Может оказаться в множестве В. А может одновременно оказаться и в множестве А и в множестве В. В этом случае оно попадает в пересечение множеств, то есть в множество А и В. Таким образом логическая операция И (логическое умножение) соответствует пересечению множеств.

Аналогично логической операции ИЛИ (сложению) соответствует объединение множеств. Если высказывание попало в множество А или оно попало в множество С, оно также лежит в множество А ИЛИ С.

И наконец логическому отрицанию соответствует инверсия. Если высказывание оказалось вне множества А, то оно лежит в множестве НЕ А. Операции И, ИЛИ, НЕ можно комбинировать. Например, выражению В И НЕ С будет соответствовать следующее множество. Все что попадает на эту площадь входит в В, но не входит в С. То есть получилось В без кусочка, относящегося к С.

Неравенства Белла можно переформулировать на языке классической логики не привязываясь к конкретным физическим реализациям вроде спинов. Обозначим высказывание «спин направлен вверх по оси 0°» за А. «Спин направлен вверх по оси 45°» за В. «Спин направлен вверх по оси 90°» за С. Отрицанию этих высказываний будет соответствовать противоположное направление спина – вниз. То есть НЕ А соответствует высказыванию «спин направлен вниз по оси 0°». И так далее. Неравенство Белла тогда перепишется в следующем виде.

Количество высказываний, входящих в А, но не входящих в В плюс количество высказываний, входящих в В, но не входящих в С больше или равно количеству высказываний, входящих в А, но не входящих в С.

Опять же доказательство тривиально. Пронумеруем области. Высказывания, входящие в А, но не входящие в В это те что попали в области 3 или 4.  Высказывания, входящие в В, но не входящие в С попадут в области 2 или 6. Высказывания, входящие в А, но не входящих в С лежат в областях 2 или 4. Наглядно видно, что неравенство удовлетворяется. Можно опять перейти непосредственно к выражению для количества высказываний. Обозначив за N1 количество высказываний лежащих в области 1, за N2, лежащих в области 2 и т.д.

Получим неравенство приводимое нами ранее:

(N3+N4)+(N2+N6)>=(N4+N2)

Вроде бы доказательство железное. Неравенство должно выполняться всегда. Но мы знаем, что оно не выполняется для некоторых квантовых систем. Выходит, что сама классическая логика не работает в случае квантовой механики. Квантовая механика оперирует Гильбертовыми векторными пространствами, а не множествами. Пересечение множеств не то же самое что пересечение Гильбертовых пространств.

Квантовым аналогом логической операции И будет умножение операторов проекции. Каждый оператор проекции задает Гильбертово подпространство. Их умножению соответствует пересечение этих подпространств. Логической операции ИЛИ соответствует сложение операторов проекции. Именно поэтому в квантовом случае мы записывали неравенство Белла в виде произведений и сумм операторов проекции. Нарушение неравенств просто показывает, что квантовая логика не идентична классической.

Она отличается от классической. И если глубоко покопаться, то окажется что изначальной причиной этих отличий являются операторы. Наблюдаемым величинам в квантовой механике сопоставляются эрмитовы операторы. Но алгебра операторов не идентична алгебре чисел. В общем случае А*В не равно В*А.   Операторы не коммутируют.

Сейчас существуют целые научные направления посвященные квантовой логике, квантовым вычислениям, квантовым алгоритмам, квантовым компьютерам и тому подобным вещам. Следует понимать что отличие квантового компьютера от классического и квантовых алгоритмов от классических не чисто условное, подразумевающее дальнейшее увеличение вычислительной мощности. Разница принципиальная. Квантовые компьютеры работают не просто на других физических принципах. Они используют другую логику.

В области IT человечество конечно продвинулось колоссально. Все начиналось с ламп, транзисторов, микросборок. Перфокарт, машинных команд, ассемблера. Теперь имеем специализированные и универсальные процессоры с сотнями миллионов транзисторов на одном кристалле. Оптику, объектно-ориентированные и функциональные языки программирования. Как сейчас модно говорить – цифровые технологии. Но следует помнить, что все они работают на той же самой классической булевской логике.

Квантовая логика и квантовый компьютер есть нечто кардинально иное.