Клеточные автоматы

Клеточные автоматы представляют собой дискретные модели с некоторым набором правил для (дискретной) временной эволюции. Проще понять на конкретных примерах. Самые простые — это одномерные клеточные автоматы Стивена Вольфрама. Пространство разбивается на клетки. В случае одномерного автомата разбивается линия. В клетке может находится либо единица, либо ноль.

Правила клеточного автомата определяют что поместить в отдельно взятую клетку в следующий момент времени. Состояние клетки в следующий момент времени определяется состоянием соседних клеток к данной. Так правило 90 по классификации Вольфрама звучит так: если соседние (справа и слева) клетки к данной одинаковые (все содержат нули или все единицы), то в клетку помещаем ноль, в противном случае (ноль справа, единица слева или наоборот) помещаем единицу. То есть фактически выполняется операция XOR с содержимым двух соседних клеток. Для приведенной выше строки следующий момент времени будет выглядеть:

Если рисовать строчки друг под другом и кодировать синим цветом единицы, а белым нули, временная эволюция такого клеточного автомата будет выглядеть как:

Мы получили фрактал — треугольник Серпинского. Это общая идея всех клеточных автоматов:

Простые правила приводят к сложной, часто непредсказуемой эволюции.

Рассмотрим, например, клеточный автомат Муравей Лэнгтона в котором «муравей» движется по двумерной дискретной поверхности согласно правилам:

• Если в клетке единица — записать в нее ноль, повернуться на 90° влево, сделать шаг вперед на следующую клетку.
• Если в клетке ноль —  записать в нее единицу, повернуться на 90° вправо, сделать шаг вперед на следующую клетку.

Исходя только из правил, не производя непосредственного моделирования, невозможно предсказать, что через некоторое время случайных блужданий муравей перейдет в «магистральное движение» (в конце видео), которое затем будет продолжаться до бесконечности.

Клеточными автоматами можно моделировать различные физические процессы. Возьмем модель DLA (Diffusion-limited aggregation), имитирующая рост кристаллов, снежинок и т.п. Правила данного клеточного автомата также очень просты:

• Частица генерируется в случайной клетке поверхности.
• Частица совершает броуновское движение до тех пор пока в одной из соседних клеток не окажется другая частица.
• Частица закрепляется в данной клетке и процесс повторяется с первого шага.

Что получается при исходной конфигурации в виде одной частицы в центре показано на видео:

Исходная конфигурация столь же важна для последующей временной эволюции как и сами правила. Возьмем наиболее известный клеточный автомат — игра «Жизнь» с правилами:

• В мертвой клетке (ноль), рядом с которой ровно три живые клетки (единицы), зарождается жизнь;
• Если около живой клетки есть две или три живые соседки, то эта клетка продолжает жить. В противном случае (если соседей меньше двух или больше трёх) клетка умирает («от одиночества» или «от перенаселённости»).

При случайном начальном заполнении получаем что-то вроде этого:

Однако, если взять некоторую специфичную конфигурацию, можно получить неповторяющуюся интересную динамику. В программе Golly собраны многие интересные конфигурации.

Исторически клеточные автоматы родились из вопроса о возможности создания машины, которая способна сделать копию самой себя. В докомпьютерную эпоху и до открытия ДНК вопрос о существовании чего-то, что может сделать точную свою копию был нетривиальным.  Знаменитый математик Джон фон Нейман решил данную задачу предложив клеточный автомат, способный создать собственную копию. Клеточный автомат получился довольно сложный: 29 допустимых состояний клетки вместо двух (единица и ноль) нами до сих пор рассматриваемых и множество правил.

За прошедшее с тех пор время автомат фон Неймана упрощали и сейчас даже клеточный автомат всего с семью состояниями (показаны цветом) может создать копию себя. Кольцо Лэнгтона, например:

Популяция таких колец ведет себя аналогично биологическим системам, то есть ими можно моделировать эволюцию и естественный отбор.

Заметьте, внутри кольца находится «ДНК», кодирующая действия автомата. То есть клеточные автоматы несмотря на свою простоту могут выполнять инструкции. Их можно программировать на определенные действия. Вот еще один, более сложный, репликатор:

Вообще-то на клеточных автоматах можно построить элементы, которые будут выполнять базовые логические операции и, следовательно, собрать затем на них компьютер. Клеточный автомат Wireworld имеет четыре состояния: пустая клетка, голова электрона, хвост электрона, проводник. Правила клеточного автомата:

• Пустая клетка → Пустая клетка;
• Голова электрона → Хвост электрона;
• Хвост электрона → Проводник;
• Проводник → Голова электрона при условии, что на соседних клетках есть ровно 1 или 2 головы электронов, иначе остаются проводниками.

Реализация двух тактовых генераторов  и вентиля XOR выглядит так:

На самом деле даже простейшие клеточные автоматы типа правила 110 по классификации Вольфрама или игра Жизнь уже являются полными по Тьюрингу. То есть для них можно найти начальную конфигурацию, которая будет выполнять логические операции из чего следует, что их можно использовать для любых вычислений — создать на их основе универсальный компьютер.

Такой компьютер конечно будет по архитектуре совершенно не похож на современные, основанные на полупроводниковых транзисторах. Вот одна из таких попыток — клеточный автомат на квантовых точках:

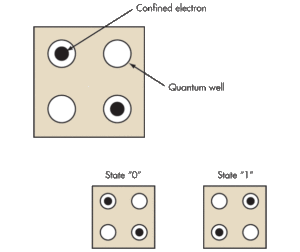
Клетка состоит из четырех квантовых точек и двух электронов. Электроны благодаря электростатическому отталкиванию стремятся расположиться либо на одной, либо на другой диагонали клетки. Диагональю можно кодировать ноль и единицу. Задание определенной начальной конфигурации также позволяет выполнять логические операции. Приведенная ниже конфигурация представляет собой инвертор, то есть операцию NOT:

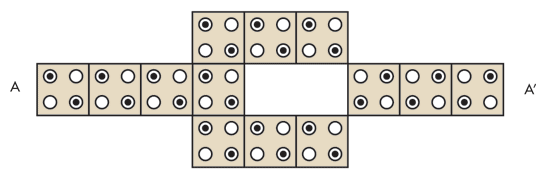
Вся логика работы основана на том, что электроны, имея одинаковый заряд, стремятся разместиться как можно дальше друг от друга.

Если дочитали до конца, поддержите автора!

Все теперь в телеграм: https://t.me/lightcone_qm