Is space and time emergent? ER-EPR correspondence adds a voice
Luboš Motl, October 22, 2013
Confused Hossenfelder and Carroll
First, let me mention things I am not going to talk about because they’re self-evidently wrong.
I won’t be talking about cosmological mechanisms behind the arrow of time because there aren’t any. The thermodynamic arrow of time (and other equivalent arrows of time) may be shown to arise from the logical arrow of time. The laws of physics allow us to determine «predictions» out of «assumptions». By definition, the laws of physics dictate how the future evolves from the past. So all the unambiguously calculable (= by the laws of physics unambiguously determined) probabilities assume that the past is known and the future is not. It follows that the probabilities in the opposite situation (future/present is known but the present/past is not) are not unambiguously calculable because they depend on priors etc.
If the laws of physics involve the time coordinate, it must agree with the existence of a chronology, an ordering of events that influence each other. The laws of special relativity guarantee that the ordering between events A,B is the same regardless of the reference frame whenever A,B may influence each other. To make this happen, relativity prohibits the superluminal communication.
However, it may be easily calculated – and it’s been calculated 17 times on this blog – that the probability of a decreasing-entropy evolution \(B^*\to A^*\) isn’t «equally high» as the probability of the entropy-increasing evolution \(A\to B\), as brutally confused people like Carroll like to say. (The asterisk stands for the CPT conjugation or just the simple T reversal when the latter is a symmetry of the theory.) Instead, the decreasing-entropy process may be seen to be less likely by an exponentially huge factor \(\exp[(S_B-S_A)/k]\). The asymmetry is due to the «summing over the final microstates but averaging over initial microstates» which is inseparable from the logical arrow of time and boils down to nothing else than the elementary probability calculus (rules that were known long before quantum mechanics).
I won’t talk about Hossenfelder’s delusions, either. Among other things, she believes that quantum gravity should produce some Lorentz-symmetry-violating terms and follows wrong papers trying to investigate the same claim. But relativity prohibits such things in all phenomena in the world, even in quantum gravity – in fact, especially in quantum gravity. The Lorentz symmetry is a principle of physics that Einstein was able to «see» through the basic empirical data available to all of us (you really can’t tell whether a train is moving if it is moving smoothly). The Lorentz symmetry constrains the «final product», the outcome of good theories’ calculations including all corrections. It doesn’t apply «just» to some zeroth-order approximations in theories; in fact, zeroth-order approximations may break the Lorentz symmetry. But when the relevant corrections are added etc., the symmetry has to be restored in the final product.
The idea of a Lorentz violation in quantum gravity is particularly silly because the word «gravity» in «quantum gravity» actually means general relativity and general relativity is obliged to preserve the Lorentz symmetry (which may be spontaneously broken if the spacetime isn’t empty, at various scales etc.). If the symmetry is broken at the Planck scale, it will be broken at any scale and one will find herself in the conflict not only with the principles that Einstein was able to guess by remembering his experiences in the train but also with much more accurate experimental tests of the symmetry: if the maximum speed that different particles may achieve differ at the Planck distance scale, they will differ at any scale!
Quantum foam: well-known geometry doesn’t have to be a part of a theory of quantum gravity
The character of the modifications of geometry that quantum gravity requires is often being misinterpreted and distorted and lots of clarifications have to be stressed to listeners who have been brainwashed by loads of crap by writers like Smolin or Hossenfelder.
First, those people want to believe you that the new quantum gravity or Planckian phenomena start to operate when the coordinate distances (or time coordinate differences) become comparable to the Planck length (or Planck time). But that definitely doesn’t happen. Relativity implies that coordinates don’t have objective physical consequences; their shortness (and value) is relative – they depend on the observer.
New quantum gravity phenomena only occur when invariant quantities with the units of length or time, e.g. the proper lengths or the radii of objects measured in their rest frame (or the impact parameter measured in the center-of-mass frame), drop to values comparable to the Planck length (or Planck time). For example, a black hole whose Schwarzschild radius approaches the Planck length marginally ceases to obey the usual laws of black holes in classical general relativity; that’s where the black holes start to intensely feel quantum mechanics and their microstates don’t differ «qualitatively» from generic unstable particles such as Higgs bosons. Black holes smaller than the Planck length don’t really exist.
On the other hand, when coordinate differences are sub-Planckian, it doesn’t mean anything new. For example, a photon’s wavelength may be 100 times shorter than the Planck length and this photon obeys all the usual properties you expect from relativity. After all, in a different inertial frame, the photon’s wavelength is much longer than the Planck scale (due to the Doppler shift).
We expect all the subleading corrections to dynamics – but only those that don’t violate the universally valid symmetries such as the Lorentz symmetry – to be comparably large to the usual «leading» terms when the typical distance scale of the physical phenomena (such as the curvature radius or the wavelength of colliding gravitational waves: it’s necessary for them to be colliding for the wavelength’s shortness to have an invariant character) approaches the Planck scale. For example, the Einstein-Hilbert action that generates Einstein’s equations of general relativity is
\[S_{EH} =\frac{1}{16\pi G} \int d^d x\, R\sqrt{-|g|}\] where \(R\) is the Ricci scalar and \(|g|\), often written simply as \(g\), is the determinant of the metric tensor (which is negative). The action above is an approximation and a more accurate formula includes corrections of higher order in the Riemann curvature tensor. For example, if we add the curvature-squared terms, we get something like
\[ S_{EH} =\frac{1}{16\pi G} \int d^d x\, (R+ c R^2+\dots)\sqrt{-|g|} \] where \(R^2\) may be the squared Ricci scalar but also other contractions of two copies of the Riemann tensor. What is the magnitude of \(c\)? It’s the point of the Planck units that in the pure gravity case, all constants of physics are expected to be of order one in the Planck units. Because \(R^2\) has units of \({\rm length}^{-2}\) times the units of \(R\) (the curvature contains the second spacetime derivatives of the metric, and otherwise just the dimensionless metric), it’s clear that \(c\) has units of \({\rm length}^{+2}\) to compensate the extra second negative power from the extra \(R\) in \(R^2\). By dimensional analysis, \(c\) must be of order
\[ c\sim \text{Planck length}^{+2}. \] When \(R\) is of order \(\text{Planck length}^{-2}\) as well, we see that the terms \(R\) and \(cR^2\) are of the same order. The Einstein-Hilbert action (and the usual term, the Einstein tensor, that it generates in the equations of motion) is no longer a good approximation for the dynamics. The subleading terms are of the same order, \(R\sim cR^2\), and the same is true for arbitrarily higher-order terms (and even the nonperturbative corrections).
So once the distances in the physical problem (e.g. the curvature radius) become comparable to the Planck length, the usual approximations we’re used to from the long-distance experience (e.g. Einstein’s equations) cease to be good and everything compatible with the universal principles (and symmetries) of physics that may happen generally will happen. But that doesn’t mean that any random science-fiction crazy idea will happen.
For example, it doesn’t mean that there is anything discrete about the geometry at the Planck scale. The word «quantum» in «quantum mechanics» was historically chosen because certain quantities (like the energy carried by photons in the electromagnetic field or the energy of the electron in the hydrogen atom) are discrete. But quantum mechanics is more general than that and many quantities (especially the position but also the momentum in a noncompact space or the energy of a free particle or an electron in/outside an ionized atom) are allowed to have and love to have a continuous spectrum. The spacetime can’t be discrete in the most naive sense because such a situation would massively contradict the Lorentz invariance – and its very accurate empirical tests.
So you should imagine that all expectations at the Planck scale are corrected by corrections of order 100 percent (if the curvature radius etc. of the problem is comparable to the Planck scale) but certain things may stay [thanks, Peter] «qualitatively the same» while other things may change qualitatively. Quantum gravity doesn’t imply that everything must change «qualitatively»; it doesn’t imply that everything stays qualitatively the same, either.
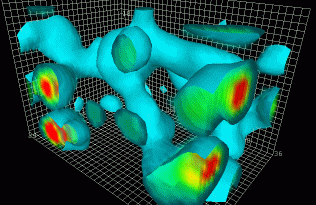
John Wheeler promoted the concept of the «quantum foam» that is pictured on the image above (I don’t mean the image of the Indian summer but the next one). If we measure \(x\) in the ground state of a quantum harmonic oscillator, we don’t get zero. Instead, we get a number that is normally distributed around zero where the width of the normal distribution is given by the width of the Gaussian (squared ground state wave function).
Similarly, if we measure the shape of the geometry with the Planckian accuracy, we won’t get a flat space. Instead, we get the wildly fluctuating quantum foam that may even contain the wormholes, as the pictures often indicate. Before string theory, there hasn’t been any formalism that would allow us to «derive» whether or not the wormholes and other topologically nontrivial modifications are really there. String theory is powerful enough to answer these questions. However, we will mostly talk about some considerations that hold in string theory but they don’t depend on its «stringiness» much. I primarily mean the ER-EPR correspondence.
We want to know: Are those bridges there in the Planckian landscape? Can we talk about the shape of the geometry at all when the resolution is this fine? Is the geometry and topology of the space a well-defined property of it? People have been asking similar questions – usually in a less careful form than my questions – for decades. Just two decades or so ago, physicists began to answer these questions. The recent findings by Susskind and Maldacena brought a new twist to all these results.
T-duality and other geometry-changing operations in string theory
The correct answer to one of the questions above is that
[A] consistent quantum theory of gravity isn’t obliged to treat the metric tensor (and the exact shape of the geometry) as a good degree of freedom at the Planckian resolution.
Only when the distances are much longer than the Planck scale, it becomes possible to isolate the «usual classical geometry» and the leading terms associated with it, such as the Einstein-Hilbert action, are much larger than all the corrections. So the physical phenomena «mostly» follow the usual rules of phenomena in a spacetime.
At the Planck scale, any of these expectations may break down. But I think it’s important to stress that they don’t have to break down. The theory – e.g. string theory (which is really the only consistent example but let me not erase the letters «e.g.», anyway) – doesn’t have to agree with the expectation that the metric tensor is a good observable at the Planck scale (and doesn’t have to answer questions about «its» values because «it» doesn’t necessarily exist). On the other hand, string theory is not obliged to agree with the proposition that the metric tensor doesn’t exist, either!
Similar comments hold about locality. Locality may be broken when the proper distances become Planckian but nothing forbids the possibility that with an appropriate field redefinition, the locality will actually hold exactly. So the breaking of the «existence of the metric tensor» and the «violations of the locality» are allowed but when they occur, they may conceivably be mere artifacts of the choice of field redefinitions, too.
The AdS/CFT correspondence describes all of type IIB string theory (supergravity, strings, branes, black holes etc.) in the Anti de Sitter (AdS) bulk in terms of a conformal field theory (CFT) on the boundary of the AdS space at infinity. The CFT is a theory analogous QCD, at least in the most famous cases in \(d=4\), and doesn’t «obviously» contain anything that would look like \(g_{\mu\nu}(\rho,x,y,z,t)\), the metric tensor in \(d=5\). However, there’s no immediate proof that such observables (the dynamical metric field in the bulk) can’t be extracted from the CFT. We usually assume that it can’t be done but there’s really no known principle that would imply that it can’t be done.
Does quantum gravity and/or string/M-theory (which is really the same thing, at the end) allow us to interpret any physical phenomena as phenomena that take place in a well-defined geometric background? What’s the shape and topology of this background?
That’s a good question, not only because it is mine and I carefully eliminated all known hidden invalid assumptions from similar questions that others could ask.
If you think about the answer, you should realize that even though a theory of quantum gravity isn’t obliged to include the metric tensor at the Planck scale among the «good quantum numbers» (well-defined degrees of freedom) at the Planck scale, the answer actually tends to be «Yes» in string theory.
In fact, string/M-theory has the tendency to allow us to interpret the same physical phenomena as physical phenomena that take place on many conceivable spacetime backgrounds, often very different spacetime backgrounds. What do I mean?
First, a gravitational wave is a particular curved configuration of the metric tensor (field) in classical general relativity. In a quantum theory, it is identified with a coherent state of many gravitons in the same one-particle state. One may build the gravitational wave – a curved spacetime metric – by adding particles (gravitons) into a flat spacetime. String theory makes this construction explicit and fully consistent (even when you ask any question about the gravitons’ interactions).
Even though string theory wasn’t obliged to provide you with a well-defined spacetime background for a given physical process, it did provide you with a well-defined spacetime background. In fact, infinitely many of them. Because a deformed spacetime may be constructed by adding graviton excitations into an undeformed (or any other deformed) spacetime, all physical phenomena in a topologically trivial spacetime may be interpreted as phenomena in any particular spacetime with the same topology (but different curvatures) equipped with different ensembles of particle-like excitations on top of the background.
Of course that we prefer the description that makes the spacetime look more empty (it is often more practical to talk about an empty curved classical spacetime than a flat spacetime with lots of gravitons in it) so one of the infinitely many descriptions of the spacetime may be more useful in practice (or more «natural» if the word «natural» is defined pragmatically). But at the fundamental level, all the spacetime geometries are equally good.
Dualities provide us with another example of the assertion that string/M-theory actually allows you to associate many background spacetimes with a given underlying process. The T-duality completely changes our ideas about the identity of the compactified circular dimensions. In one of the T-dual (and therefore mutually equivalent) descriptions, the compact dimension \(X^{10}\) is complementary to the momentum \(P^{10}\) of the strings or other objects. But there is another description in which the compact dimension is \(\tilde X^{10}\) which is complementary to \(\tilde P^{10}=W^{10}\), the winding number of strings around the original dimension \(X^{10}\).
These two directions, \(X^{10}\) and \(\tilde X^{10}\), aren’t fully compatible with one another. We can’t imagine that the strings are moving in a spacetime that has both of these dimensions, \(X^{10}\) and \(\tilde X^{10}\), at least not strings that are moving and winding in the usual largely unconstrained way. However, both descriptions, one with \(X^{10}\) and one with \(\tilde X^{10}\), are equally valid, equally legitimate, and offer us equally accurate frameworks to calculate all the physical predictions.
A special kind of T-duality is the mirror symmetry – which may be interpreted as a T-duality «reverting» the three coordinates of the \(T^3\) fibers if the Calabi-Yau manifold is written as a fibrations – and it implies that two topologically different Calabi-Yau manifolds produce the same physics. For example, some physical phenomena in type IIA string theory may be thought of as taking place in a spacetime with one Calabi-Yau manifold whose Hodge numbers are \((h^{1,1},h^{1,2})\). There exists an exactly equivalent description of these phenomena as type IIB string theory phenomena on a topologically different Calabi-Yau manifold with the reverted Hodge numbers \((h^{1,2},h^{1,1})\). None of them is better than the other. None of the geometries is «more real» than the other (at least when all the distance scales are comparable to the string length – which is the self-dual radius for a T-duality; it’s not the Planck length). Both of them work but the dimensions (at least 3 of the 6 dimensions) in the two descriptions are incompatible with each other. They’re different spaces. They’re not projections of the same 9-dimensional or 12-dimensional space, for example.
The S-duality only acts on «internal» properties of the particles (light excitations and monopoles are interchanged, for example), but it preserves the spacetime in which they are embedded. However, U-dualities – more general duality transformations that act on internal as well as geometric quantities, i.e. they combine the actions known from S-dualities and T-dualities – do switch the background to a different one. That’s also the case of the \(E_{k(k)}(\mathbb{Z})\) discrete exceptional non-compact U-duality symmetries in M-theory on tori (with maximally supersymmetric supergravity at low energies). The compactified dimensions in all the infinitely many spacetimes related by these U-duality transformations are different. The momenta in the compact directions are equal to the M2-brane and M5-brane winding numbers (and more complicated charges) in the U-dual, equivalent descriptions (or their linear combinations).
The string-string duality (the heterotic-K3 duality) is yet another example of the fact that string theory often provides us with numerous exactly equivalent descriptions of the same physical phenomena that may disagree – even completely disagree – about the identity of the spacetime background, even about its topology. The AdS/CFT correspondence in particular or holography in general is yet another example in which the two equivalent descriptions may disagree about the number of spacetime dimensions, too. To ask whether the radial holographic dimension «exists» means to ask the question whether you prefer the AdS or the CFT description. If you’re impartial enough, you know that you shouldn’t take sides. They’re equivalent.
In most of the interesting stringy cases, we’re not dealing with two descriptions among which one of them is much more accurate (or much more symmetric) than the other and the other is just an approximation (or a contrived broken phase). Instead, both of the dual (equivalent) descriptions are equally accurate, they often have equal numbers of dimensions, they often have comparable symmetries (my favorite example is the \(SO(32)\) and \(E_8\times E_8\) heterotic string theory that are T-dual to each other if one correctly adjusts the Wilson lines and other parameters; one can’t say that one of the gauge groups is a broken version of the other one – in fact, both groups have rank \(16\) and dimension \(496\)); there’s no way to present one of them as «superior» in any way. In some sense, they are connected with different but equally good classical limits of the full quantum theory.
So I have mentioned many examples of insights, dualities, and constructions in string/M-theory that seem to support the same general story: Even though string/M-theory isn’t obliged to provide us with a spacetime interpretation of physical phenomena, it always tends to give us a spacetime background for any phenomena that may occur. In fact, it’s not just one spacetime but many (and because of the coherent graviton states we started with, and also because of the infinite order of the non-compact U-duality groups in M-theory, infinitely many) spacetime frameworks for any events.
At the beginning, we were warned that quantum gravity had the right to make all of our concepts and ideas about the spacetime background meaningless once we demand the Planckian resolution. For given physical processes in the quantum gravity regime, it could happen that no spacetime background was OK. But instead, the final result seems to paint a different story. It is possible to use a spacetime background – in fact, one may do so in many ways. In some sense, any event may be described as a more or less convoluted rearrangement of particles on any spacetime background.
Possibility to fix the gauge (light-cone gauge) in string theory & allowed topology change & ER-EPR
When you looked at the picture of the quantum foam at the top, you could have been afraid that these wormholes that may appear at the Planck scale will prevent us from describing a generic accurate nonperturbative process in quantum gravity as a process that occurs on a topologically trivial background. After all, doesn’t the picture make it obvious that the right spacetime’s topology is not trivial which should mean that every description in terms of a trivial topology must be wrong – or at least inaccurate?
As the previous long section suggested, the answer may be surprising but it shows the tremendously strong muscles of string/M-theory. The answer is that string theory allows you to use the background you choose, even the flat one, and describe all the phenomena completely accurately (not just in a perturbative approximation) even though the theory may also endorse the picture in which there are many wormholes.
The reason is that the spacetime topology isn’t a well-defined quantum number. It is not associated with any well-defined linear operators on the Hilbert space! Some particular ket vectors in the Hilbert space may be «suggestive» of one spacetime topology but their linear superpositions may prefer a completely different topology!
So string theory works perfectly even if you try to «impose» an arbitrary spacetime geometry – and topology – on it. It may just make a particular process look more contrived than it is in a different description. Particular configurations may be closer to the «ground state» of one spacetime background and the corresponding interpretations may be pragmatically preferred. Some spacetime backgrounds may be preferred over others (in which a physics problem may be described equivalently) because they have lower values of the coupling constants or longer radii (or smaller curvatures). But fundamentally speaking, none of them is «qualitatively» better than others.
I’ve been sure about the string/M-theory’s consistency – up to arbitrarily short distance scales – in a flat background (a theory seemingly «prohibiting» the different topologies) since the 1996 discovery of Matrix theory by Banks, Fischler, Shenker, Susskind. Why did Matrix theory settle these viewpoints of mine?
Well, in the early 1980s, Green and Schwarz were using the light-cone gauge when they were igniting the First Superstring Revolution. The light-cone gauge apparently allows you to slice the spacetime into null slices
\[ x^- = {\rm const} \] and all the interactions of strings may be described in this way. A good feature of a slicing is that it allows you to define a Hamiltonian. If you study string theory covariantly, i.e. you only ask about quantities that make the Lorentz symmetry manifest, you may see that string theory only calculates on-shell quantities (the scattering amplitudes in the S-matrix). The off-shell Green’s functions (defining finite-delay response functions etc.) aren’t well-defined. This has been known to be OK – in fact, it is a property exemplifying string theory’s ability to teach us basic things about gravity – because the diffeomorphism symmetry makes the location of a field operator gauge-dependent so gauge-invariant (or gauge-covariant) correlators can’t be associated with «fixed» spacetime points. The S-matrix formalism only gives us the unitary evolution operator \(S\) from \(t=-\infty\) to \(t=+\infty\).
But the light-cone gauge seems to overcome this limitation. It seems to give us a well-defined Hamiltonian \(H=P^-\) (using the light-like slicing) which may be exponentiated to produce the unitary operator for any finite or infinite delay, \(U=\exp(-iH\cdot \Delta t)\). The light-cone gauge makes the Lorentz symmetry a bit harder to prove and the diffeomorphism symmetry (and analogously, other gauge symmetries) are being obscured (they’re not a part of this formalism at all, to be more accurate, because the light-cone gauge eliminates all the unphysical redundant degrees of freedom from scratch). But if you care about the finite-time evolution and the manifest absence of bad ghosts (negative-norm states), the light-cone gauge seems to be a way to go.
However, in the 1980s, it was conceivable that the light-cone gauge was only consistent in the perturbative approximation – and only for processes for which the initial spacetime background (typically the Minkowski flat spacetime) is perturbed at most infinitesimally. Can the same light-cone gauge describe processes in which the spacetime is heavily curved (by many gravitons) and for which \(g=O(1)\) which also means \(\ell_{\rm string}\sim \ell_{\rm Planck}\)?
Matrix theory – and matrix string theory – answered these questions in the affirmative. The gauge works perfectly at any \(g\) – matrix string theory is a complete, non-perturbative definition of type IIA string theory at any value of \(g\) – and there is clearly no limitation on the number of gravitons you may add to the state, either. So at least the light-cone gauge (and perhaps, but not necessarily, other gauges) is a consistent description of a theory of quantum gravity in a nearly flat spacetime background, even at an arbitrarily strong coupling and an arbitrary energy density.
All these developments support the general theme that string/M-theory gives us the freedom to «impose» any spacetime background we wish and there will be a consistent description of the phenomena, anyway. In fact, it seems that you may even start with a background violating some laws (e.g. classical equations) and the stringy-braney matter will do its job to fix the bugs and list all the possibilities for configurations that are actually kosher (and their evolution).
In the early 1990s, this theme was also supported by the discovery of the topology-changing transitions in string theory that are completely smooth and consistent. One Calabi-Yau manifold was shown to be able to change to a topologically distinct one by going through a geometrically singular but physically well-defined and fully consistent intermediate point (a conifold). The milder flop transitions (which preserve the Hodge numbers but rearrange the cycles into their combinations) and the more severe conifold transitions (which do change the Hodge numbers and connect all or almost all Calabi-Yau manifolds into a connected web) may also be described as a condensation of wrapped D-branes on the shrunk cycles (or processes occurring on them have extra world sheet instantons wrapped on the shrunk cycles). In this sense, any state «on top of» the Calabi-Yau manifold of the second topology may be described as a state (including wrapped D-branes) on the Calabi-Yau manifold of the first topology and vice versa.
Again, this freedom to think about the topology of the Calabi-Yau background agrees with the general lesson that string/M-theory gives us the freedom to «choose» the spacetime background without losing an iota of the consistency and accuracy of the description of the resulting physical phenomena.
Maldacena and Susskind: don’t be afraid to start with a vastly different spacetime
This general point is strengthened by the recently articulated ER-EPR correspondence by Maldacena and Susskind. They phrase the insight as an alternative description of the entanglement (popularly associated with the acronym «EPR» of physicists who popularized it and demonized it) and with a non-traversable wormhole (the Einstein-Rosen bridge).
In this description, one is dividing physical states to «spooky ones» and «ordinary ones» which introduces a clear asymmetry to our emotions. The unentangled black holes are the «ordinary ones» while a wormhole is spooky; and any general entanglement is also spooky. This is a popular way to present the correspondence – especially because the readers, and not only the complete laymen, have been brainwashed by decades of books painting entanglement as a «spooky thing». And the wormholes (even the non-traversable ones which are almost certainly allowed) have been largely underdebated in the literature. So the ER-EPR link identifies two spooky or bizarre things with one another.
If you subtract this low-brow laymen’s bias and realize that there is nothing spooky about the entanglement (or about different topologies), you may formulate the ER-EPR correspondence in a more symmetric and more rational (my) way. It says that
The Hilbert space \(\mathcal{H}_{ER}\) of the states of an Einstein-Rosen bridge, including all possible excitations of matter in the bridge, is the same Hilbert space as the Hilbert space of the two disconnected black holes at the same locations, \(\mathcal{H}_{BH1}\otimes \mathcal{H}_{BH2}\). These are just two ways to interpret the very same quantum states in the same theory, two ways to associate them with different spacetime backgrounds.
This meaningful beef of the proposition above is exactly equivalent to the correspondence as formulated by Maldacena and Susskind. But the two Hilbert spaces that are said to be equivalent are treated much more symmetrically. The two Hilbert spaces are the same for one bridge or a pair of two black holes. Just the states of the two black holes that have a lower entanglement entropy may be presented more meaningfully as states of two black holes; the higher-entangled states are more pragmatically described as states of the single Einstein-Rosen bridge.
Equivalently, the states with a nearly empty Einstein-Rosen bridge are more meaningfully described as not too violent excitations of an empty Einstein-Rosen bridge; the strongly excited Einstein-Rosen bridges correspond to bridges that tend to «chop off» and resemble the two independent black holes.
You see that the ER-EPR correspondence is the latest salvo in the same theme: string/M-theory allows you to choose many different spacetime backgrounds if you want to describe the same physical phenomena. But there’s a sense in which the ER-EPR correspondence goes beyond all the previous examples (coherent states of gravitons, T-duality, mirror symmetry, heterotic-K3 duality, AdS/CFT correspondence, conifold transitions). What is it?
In all the previous examples that showed that the character of the spacetime could have been modified, the time didn’t really play any substantial role. The two (or many) spacetime backgrounds whose physics was claimed to be equivalent were actually using the same spacetime coordinate (or at most a mildly curved one, in the case of the coherent state of gravitons). The bulk of all these dualities and similar relationships could have been described in stationary situations.
But in the ER-EPR correspondence, time plays an essential role for the first time. There is no natural way to choose the time coordinate in a way that would apply to both equivalent descriptions (two isolated black holes; one bridge). Despite the fact that the equivalent description changes the shape and topology of the spacetime in a way that can’t be reduced just to a change of the shape and topology of the space, the two descriptions are still perfectly equivalent.
This seems to imply that the lessons about the «allowed topology change» in string theory that we have learned from the previous examples does generalize to the case of the spacetime (and time), too. The chronology of events (or knowledge about observables) must still be preserved and all the valid equivalent descriptions will agree about them. But the precise way to connect them and embed them into a spacetime doesn’t have to be unique. Whatever way you choose, string/M-theory will offer you a valid description of the physical phenomena. You should never be afraid of choosing a background. String theory will work independently of the background and give an interpretation for the phenomena.
So are the space, time, and spacetime doomed?
I think that the answer is the following: Although it could have happened that quantum gravity could have banned the usage of spacetime geometries in the accurate treatments of situations and processes (in the Planckian realm), the actual evolution of quantum gravity and string/M-theory seems to paint a different story.
We are actually allowed to use a spacetime background, even if you want to describe or predict the most generic or extreme processes absolutely accurately. In fact, we may use (almost) any spacetime background to describe (almost) any physical processes.
Allowed topology changes (e.g. conifold transitions) may always be described as a condensation of objects on the original background; allowed (non-traversable) wormholes may be described as entangled states of objects (on a wormhole-free background) whose details reflect the properties of the wormhole.
So what is doomed isn’t a spacetime in the sense of our right of using the concept; what is doomed is the idea that a classical spacetime is unambiguously associated with states or processes. The association is not only refusing to be unique but to a large extent, the spacetime may be chosen arbitrarily (even its topology may be chosen differently, even if the topology change involves time in a nontrivial way). An inconvenient choice of the spacetime background for a given physical situation will be manifested in the complexity of the collections of particles and objects that live on top of the chosen spacetime but the theory will never say that the choice is «fundamentally wrong».
So the advances in string/M-theory and quantum gravity have eliminated the idea that the reality canonically carries a «particular spacetime background». At the fundamental level, the separation of the reality to the «spacetime» and «the objects that live on the spacetime» is highly redundant if not arbitrary. This fact may be viewed as a manifestation of the inevitable unification of gravity with other forces or matter. You just can’t objectively or canonically determine which part of the state or process or reality is gravity (space and time); and which part is the information about the objects or phenomena taking place on that background! Only some combination of theirs retains its unambiguous meaning.
The relationship with the amplituhedron was already discussed: Similar constructions may make the spacetime look totally obscured but the ultimate reason why the amplituhedron is more important than other generic polytopes is that it has implications for phenomena in a spacetime – relationships between knowledge of observables associated with spacetime points or regions – in fact, phenomena in many spacetimes. A spacetime will always be able to pump life into mathematical results (although it may be done in many ways). Without any spacetime, claims about mathematical structures will always remain pure maths or – using a physicist’s perspective – unphysical tautologies.