Спин электрона. Часть 5 – Принцип суперпозиции. Кубит.
Первая часть про спин здесь.
Спин электрона ведет себя очень странно. Математически описывается абстрактными векторами состояния. Мало того, что при измерении спин оказывается в состоянии собственного вектора спиновой матрицы, до измерения он может описываться еще сложнее. Мы всегда неявно предполагали, что первое измерение спина уже произведено. Нельзя просто взять электрон и предположить, что его спин уже описывается таким-то вектором состояния. Надо сначала пропустить его через прибор Штерна-Герлаха или еще каким-нибудь способом измерить спин. Это называется подготовка состояния. С этого момента мы можем применять математический аппарат квантовой механики для предсказания результатов будущих измерений, например посчитать какова вероятность того, что находясь в состоянии \( \displaystyle|\psi\rangle\) он окажется в состоянии \( \displaystyle|\varphi\rangle\). Необходимо найти амплитуду вероятности \(\displaystyle \langle\varphi|\psi \rangle\) и возвести ее модуль в квадрат. Странно, но вектор состояния между измерениями может находится не только в одном из базисных. Он способен быть в любой из их суперпозиции. Опять же математику проще пояснить на примере обычных векторов на плоскости.
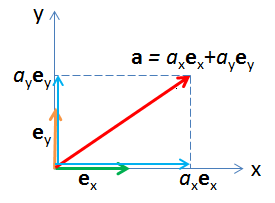
Векторы \(\displaystyle \boldsymbol{e}_{x}\) и \(\displaystyle \boldsymbol{e}_{y}\) это базисные векторы декартовой системы координат:
\(\displaystyle \boldsymbol{e}_{x}=\binom{1}{0}\),
\(\displaystyle \boldsymbol{e}_{y}=\binom{0}{1}\)Любой вектор на плоскости можно представить суперпозицией (суммой) базисных, умноженных на соответствующую координату \(\displaystyle a_{x}\) и \(\displaystyle a_{y}\):
\(\displaystyle \boldsymbol{a}=a_{x}\boldsymbol{e}_{x}+a_{y}\boldsymbol{e}_{y}=a_{x}\binom{1}{0}+a_{y}\binom{0}{1}=\binom{a_{x}}{a_{y}}\)Причем сама координата — это не что иное как скалярное произведение самого вектора с базисным. Геометрическая интерпретация скалярного произведения это проекция одного вектора на другой. Проекция на ось координат таким образом и есть координата:
\(\displaystyle a_{x}=\boldsymbol{e}_{x}\cdot\boldsymbol{a}=\begin{pmatrix}1 & 0
\end{pmatrix}
\binom{a_{x}}{a_{y}}\)
С векторами состояния все происходит по аналогии. У нас есть базисные векторы, скажем «спин вверх» \( \displaystyle |\uparrow\rangle\) и «спин вниз» \( \displaystyle |\downarrow\rangle\). Только их мы можем получить при измерении спина относительно оси z. Но наиболее общим вектором является суперпозиция:
\( \displaystyle |\psi\rangle= c_{\uparrow}|\uparrow\rangle+c_{\downarrow} |\downarrow\rangle\)где \( \displaystyle c_{\uparrow}\) и \( \displaystyle c_{\downarrow}\) это компоненты вектора состояния — просто числа (в общем случае комплексные числа). Как и в случае с обычными векторами на плоскости, компонента это скалярное произведение вектора с базисным. Но скалярное произведение в квантовой механике это ни что иное как амплитуда вероятности:
\( \displaystyle c_{\uparrow}=\langle\uparrow|\psi\rangle\)Выходит, что квадрат модуля компоненты вектора состояния это вероятность при измерении обнаружить спин в данном базисном векторе и измерить собственное значение этого вектора. То есть в нашем случае \( \displaystyle |c_{\uparrow}|^{2}\) это вероятность получить спин «вверх», а \( \displaystyle |c_{\downarrow}|^{2} \) спин «вниз». Поскольку другого варианта не дано, то в сумме вероятность должна равнятся 100%:
\( \displaystyle |c_{\uparrow}|^{2}+|c_{\downarrow}|^{2}=1\)Это так называемая нормировка вектора состояния. Она обобщается на случай когда компонент вектора больше двух. Например, следующий вектор состояния говорит, что при измерении спина относительно оси z, 50% окажутся со спином «вверх» и 50% со спином «вниз»:
\(\displaystyle|\psi\rangle=\frac{1}{\sqrt{2}}(|\uparrow\rangle+|\downarrow\rangle)\)
В чем же заключается важность принципа суперпозиции? С точки зрения обычных векторов на плоскости ничего необычного не происходит. Однако если вспомнить, что векторы состояния это не направленные отрезки, а абстрактное описание физической системы (спин электрона в нашем случае), то видно что происходит что-то странное. Общий вектор состояния складывается из части, содержащей спин «вверх», плюс части, содержащей спин «вниз». Но при наблюдении спина мы никогда не получим суммы. В результате измерения мы получим либо \( \displaystyle |\uparrow\rangle\) с вероятностью \( \displaystyle |c_{\uparrow}|^{2}\) либо \( \displaystyle |\downarrow\rangle\) с вероятностью \( \displaystyle |c_{\downarrow}|^{2}\). То есть происходит необратимый коллапс вектора состояния. Исходный вектор состояния ненаблюдаем. Невозможно измерить числа \( \displaystyle c_{\uparrow}\) и \( \displaystyle c_{\downarrow}\) не разрушив исходный вектор. Иногда такую квантовую систему с двумя состояниями представляют вектором на сфере Блоха:
Благодаря условию нормировки вектор получается единичной длины, а углы можно выразить через компоненты вектора состояния. Такое представление с одной стороны наглядно, но с другой стороны еще больше запутывает. Вектор состояния спина — это не обычный вектор в виде направленного отрезка. Кстати, спин электрона является одной из физических реализаций кубита: квантовомеханической системы с двумя состояниями (квантовый бит=quantum bit=qubit=кубит). Если обозначить «вверх» за «1», а «вниз» за «0», получим тот самый кубит. Тут можно интуитивно понять отличия и «встроенный параллелизм» квантовых компьютеров: классический бит не может в отличие от квантового находится в суперпозиции нуля и единицы. Всякие обобщения квантовомеханических понятий на макроскопический уровень приводят к парадоксам типа кота Шредингера в состоянии \( \displaystyle |жив\rangle+|мертв\rangle\). Хотя такое состояние ненаблюдаемо даже в квантовой механике. При измерении мы получим или \( \displaystyle |жив\rangle\) или \( \displaystyle |мертв\rangle\). Но суперпозиция квантовомеханических состояний влияет на результаты экспериментов. Это еще одна странность математического аппарата квантовой механики — в ее промежуточных расчетах фигурируют принципиально ненаблюдаемые величины.