Производная и оператор дифференцирования
Значение дифференциального и интегрального исчислений сложно переоценить. Фактически современная наука и началась с открытия Ньютоном законов механики и разработки им же соответствующего математического аппарата для анализа следствий этих законов. С тех пор математика была и остается тесно переплетенной с физикой. Иногда для физики используется разработанный математиками аппарат, как в случае с общей теорией относительности Эйнштейна. Иногда физики из своих соображений приходят к новым математическим структурам, например, так было с обобщенными функциями, первую из которых ввел Дирак для нужд квантовой механики.
Производная и интеграл основаны на понятиях о бесконечно малых и возможности деления отрезка до бесконечности. С точки зрения физики существование минимальной длины противоречит теории относительности, ведь разные наблюдатели увидят разную длину. Так же есть веские основания полагать, что деление отрезка до бесконечности тоже невозможно, поскольку понятие длины теряет свой смысл на малых расстояниях (порядка \( \displaystyle 10^{-35}\)м.). Несмотря на это вся современная наука (в том числе квантовая механика и теория струн) пропитана дифференциальным исчислением. Даже дискретные результаты типа квантования энергетических уровней атомов получаются из рассмотрения непрерывных функций и дифференциальных уравнений.
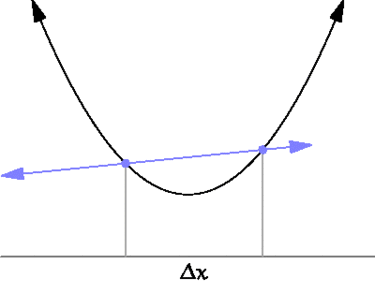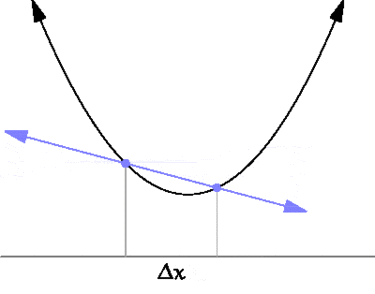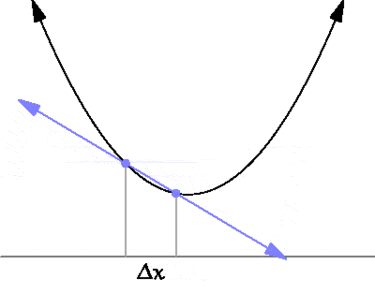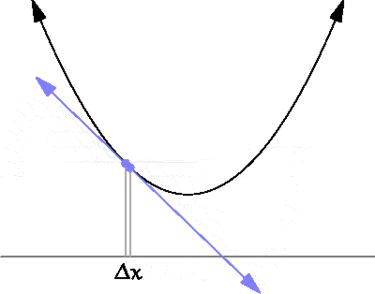
Производная функции в какой-либо точке по определению это отношение интервала \( \displaystyle \Delta y\) к интервалу \( \displaystyle \Delta x\) в окрестности этой точки, когда длины этих интервалов стремятся к нулю. На рисунке для примера показаны две точки с соответствующими интервалами.
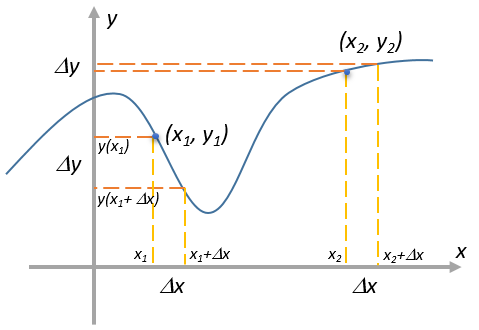
Хотя сами интервалы в пределе бесконечно малы, их отношение в общем случае имеет конечную величину:
\( \displaystyle f'(x)=\frac{dy}{dx}=\frac{\Delta y}{\Delta x}\) при \( \Delta x\rightarrow 0\)
где через \( \displaystyle dx\) и \( \displaystyle dy\) обозначают дифференциалы (difference — разность), то есть те самые бесконечномалые интервалы — разность декартовых координат текущей и следующей точек.
В научной литературе обозначение производной штрихами практически не используется, а запись в виде отношения дифференциалов общепринята. По сути это и есть определение производной.
Из рисунка видно, что даже при одинаковом \( \displaystyle \Delta x\) соответствующая величина \( \displaystyle \Delta y\) будет разной. Каждой точке непрерывной функции \( \displaystyle f(x)\) можно сопоставить число — производную функции в этой точке. Совокупность этих точек тоже будет непрерывной функцией — производной исходной функции.
Физическим смыслом производной является скорость изменения исходной функции. Достаточно взглянуть на рисунок выше чтобы понять. В районе первой точки функция быстро меняется. Производная будет иметь большую величину потому что \( \displaystyle \Delta y\) большое. И она будет отрицательной, так как \( \displaystyle y(x_{1}+\Delta x)<y(x_{1})\) и их разница \( \displaystyle \Delta y = y(x_{1}+\Delta x)-y(x_{1})\) будет отрицательной. Для второй точки, где функция почти не меняется, производная мала так как \( \displaystyle \Delta y\) мало. Если функция вообще не меняется (постоянна — constant — константа), то производная равна нулю, т.к. \( \displaystyle \Delta y=0\). Если функция идет «вверх» — производная положительна. Если «вниз» — отрицательна. Понятно, что в точках перехода из «вверх» в «вниз» производная будет равна нулю. То есть в точках экстремума (максимум или минимум) исходной функции производная равна нулю.
Производная функции в точке также связана с касательной к этой точке. Если провести через точки \( \displaystyle y(x)\) и \( \displaystyle y(x+\Delta x)\) прямую, то она будет касательной в пределе \( \Delta x\rightarrow 0\).
Для элементарных функций их производные можно найти прямо из определения. Так, например, для функции \( \displaystyle y(x)= x^{2}\) производная равна:
\( \displaystyle \frac{\Delta y}{\Delta x}=\frac{(x+\Delta x)^{2}-x^2}{\Delta x}=\) \( \displaystyle \frac{x^2+2x\cdot \Delta x +\Delta x ^{2}-x^2}{\Delta x}=\) \( \displaystyle 2x+\Delta x=2x\) при \( \displaystyle \Delta x\rightarrow 0\)
В реальной жизни, при численных вычислениях на компьютере, к пределу \( \displaystyle \Delta x\rightarrow 0\) вообще не переходят. Скажем, с микрофона поступает аналоговый сигнал \( \displaystyle f(t)\), который необходимо оцифровать с частотой \( \displaystyle 1/\Delta t\) и произвести цифровую обработку в которой как раз и используются производные. Сигнал (функция) разбивается на конечное число точек (дискретизация):
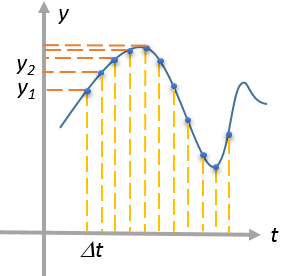
Декартовы y-координаты этой дискретной функции можно записать в вектор-столбец:
\( \displaystyle f(t)=\begin{pmatrix}y_{1}\\
y_{2}\\
y_{3}\\
…\\
y_{n}
\end{pmatrix}\)
А взятие производной можно записать в виде умножения матриц:
\( \displaystyle \frac{d}{dt}f(t)=\) \( \displaystyle \frac{1}{\Delta t}\begin{pmatrix}
-1&1 &0 &… &0 \\
0&-1 &1 &… &0 \\
0&0 &-1 &… &0 \\
…&… &… &… &…\\
0& 0& 0& …&1
\end{pmatrix}\begin{pmatrix}
y_{1}\\
y_{2}\\
y_{3}\\
…\\
y_{n}
\end{pmatrix}=\) \( \displaystyle \frac{1}{\Delta t}\begin{pmatrix}
y_{2}-y_{1}\\
y_{3}-y_{2}\\
y_{4}-y_{3}\\
…\\
y_{n}-y_{n-1}
\end{pmatrix}\)
Кажется громоздко, но смысл прост. Это просто произведение квадратной матрицы на вектор-столбец (исходная функция), которое дает другой вектор-столбец (производная функция). То есть получившийся вектор-столбец как раз будет являться аппроксимацией производной исходной функции. Проверьте, что умножая приведенную матрицу по стандартному правилу «строка на столбец» мы получим вектор, состоящий из разниц значений функции в соседних точках, например: \( \displaystyle \Delta y_{12}=y_{2}-y_{1}\) и т.п., что по определению и есть производная (если поделить на \( \displaystyle \Delta t\)). Это еще одна наглядная демонстрация откуда пошло название дифференциал (разность по-русски), достаточно посмотреть на вектор-столбец результата.
Заметьте, что мы свели операцию взятия производной к простому умножению матриц. Если вектор-столбец является аппроксимацией функции, то приведенная матрица (деленная на \( \displaystyle \Delta t\)) — это аппроксимация самого оператора дифференцирования \( \displaystyle \frac{d}{dt}\).
То есть при \( \displaystyle \Delta t \rightarrow 0\) матрица и вектор-столбец будут бесконечномерными и мы перейдем от аппроксимации к действительным величинам: функциям и операторам над ними. То есть оператор и матрица фактически одно и тоже в нашем контексте. Кстати, матрицами можно представлять и более простые операции.
Одной из точек зрения на процесс взятия производной (дифференцирования) является взгляд с позиции линейных операторов. Оператор (operator — выполняющий операцию) это то, что действует на функцию в результате чего получается другая функция. По прямой аналогии примера с матрицами, алгебраически можно записать:
\( \displaystyle \hat{D}f(t)=f'(t)\)где за \( \displaystyle \hat{D}\) обозначен оператор дифференцирования \( \displaystyle \frac{d}{dt}\).
Читать следует так: оператор \( \displaystyle \hat{D}\) действует на исходную функцию \( \displaystyle f \) в результате чего получается другая функция \( \displaystyle f’\). Действие оператора можно представить графически как изменение сигнала неким преобразователем:
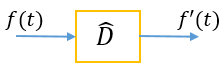
Поскольку другие операторы, в том числе и элементарные (сложение, умножение), можно записать в подобном графическом виде, данная парадигма позволяет наглядно отображать дифференциальные уравнения в виде схем и производить их численный анализ на компьютере. Известный пример реализации — Simulink в составе MATLAB.



«Так же есть веские основания полагать, что деление отрезка до бесконечности тоже невозможно, поскольку понятие длины теряет свой смысл на малых расстояниях (порядка 10−35м.).»
Деление «отрезка», до бесконечности — возможно. Это математический объект.
А вот, деление «метра», до бесконечности , это физикам решать.
Хотя, даже… понятие «отрезок», как такой математический объект, на котором можно расположить бесконечно точек, под сомнением….
Ведь, если их расположили бесконечное число, он должен коллапсировать в точку.
Ну… — какова высота стопки бумаги, из бесконечного числа листов, если каждый из них имеет толщину равную нолю?
Но мы его, сразу, представляем себе, как объект состоящий из точек… а не ставим две точки А и В, назвав их — «отрезок».
И математическая «аксиома полноты», со своим утверждением о том, что — любой точке математической прямой соответствует вещественное число. Если это так, то математическая прямая коллапсирует в точку.
Ну, по крайней мере, если решить их все расположить сразу на прямой, то будет всё в точке.
И она, «математическая прямая», невозможный объект, как и отрезок… Но можно располагать точки, по неким правилам относительно друг друга… с некими промежутками… Но не все сразу.
Ситуация такова, что имея «абсолютно точную линейку», ну, или стремясь «абсолютно точно измерить нечто», ты ничего кроме ноля получить не можешь.)))
А ничего не измеряя, ты имеешь — континуум — непрерывность, или бесконечность…
Любой объём континуума, содержит бесконечно точек, которые если посчитать, то этот объём уйдёт в коллапс.
Что касается «бесконечно больших», и как предел — бесконечность, ну пусть неких единиц… откладываемых на прямой… Если такое число взять единовременно, то все ваши единицы пропадут, их сожмёт до нулевого расстояния между ними, и… коллапс.
Аналогично и во времени….
Если ты ничего не измеряешь, по времени, то у тебя есть вечность, а абсолютное точное измерение приводит тебя в неизменности во времени — мгновению. Парадокс Зенона.
Где, в каждом отдельном мгновении стрела — покоится… А вообще — летит.
Вот, вам, уже — пространственно-временная нелокальность.
Чтобы было какое-либо движение должна быть пространственно-временная нелокальность.
И на микро и на макро уровне.
Вообще, математически, в любое расстояние, или объём, сколь угодно малый, по пространству, отличный от нуля можно вместить любое количество информации отличное от бесконечности.
Аналогично и в любой, сколь угодно малый интервал, во времени…
И не важно, что с точки зрения физики, это воспринять нет возможности.
С другой стороны, с точки зрения Вечности, — во времени, и Бесконечности — в пространстве — вселенной не существует.
Или, как минимум, нет её конкретной пространственно-временной локализации, как и любого объекта в ней…
Ну, это математически… Ну, или по Буддизму)))
Ну, и если пошёл разговор о нелокальности, и в более общем случае — неопределённости…
____
То математики, стремясь решить проблему V -1 , получили неопределённый объект — i — мнимое число.
Которое если i * i, то = -1, но какое i из этой пары является «положительным», а какое «отрицательным» — неизвестно. Ну, в том смысле — какое i представляет собой -1, а какое +1. Вернее — известно, что с вероятностью 0,5.
Аналогично и для — -i * -i = -1 — вероятность 0,5.
Что верно и для произведений: i*-1 =1, -i*i=1 — с вероятностью 0,5, оба i подразумевают +1, и с аналогичной вероятностью , что содержат -1.
Комплексные числа — вероятностные объекты, с заданной вероятностью.
Как и кватерионы, октонионы, седенионы… неопределённость возрастает…
Но если бы это всё…
___
Оказывается? что введение i приводит к возникновению следующей ситуации V 1 , теперь это не плюс-минус единица, а ещё и i*-i, как и -i * i.
То есть:
1,
-1,
i * -i,
-i * i.
Это можно и не замечать…
У вас, при вычислении корня из 1, получается два вероятностных объекта, с которыми нужно что-то делать, аналогично тому, как поступили с корнем из -1, где было две пары — 1*-1 и -1*1.
____
Теперь вам, для того, чтобы решить эту новую проблему с V 1 , нужно создавать новый класс чисел, с большей неопределённостью. _____
Что, в свою очередь, вас вернёт обратно к V -1 с аналогичной четвёркой вариантов, от которой ушли…
И вас затягивает в водоворот наращивания неопределённости…
Технически… для вычислений, наверное, проблемы не возникает… но вам нужно понимать логические следствия… Возможно, если они будут осознаны, то откроется что-то новое в математике…
Ну, например, пространство Римана, тогда может начать принимать новые свойства, с каждым таким витком….
тексте «V» — корень квадратны. Просто текст, при отправке меняет форматирование… и черту корня сдвнуло.