Спин электрона. Часть 1 — Эксперимент Штерна-Герлаха.

Спин (spin – вращение) это наиболее простая вещь на которой можно продемонстрировать отличия квантовой механики от классической. Из определения кажется, что связан он с вращением, но не надо представлять себе электрон или протон вращающимися шариками. Как и в случае многих других устоявшихся научных терминов было доказано что это не так, но терминология уже устоялась. Электрон – точечная частица (нулевого радиуса). А спин отвечает за магнитные свойства. Если электрически заряженная частица движется по кривой траектории (в том числе вращается), то образуется магнитное поле. Электромагниты так работают – электроны движутся по проводам катушки. Но спин отличается от классического магнита. Вот неплохая анимация:

Если магнитики пропускать через неоднородное магнитное поле (обратите внимание на различную форму северного и южного полюсов магнита, задающего поле), то в зависимости от ориентации магнитика (его вектора магнитного момента) они будут притягиваться (отталкиваться) от полюса с большей концентрацией силовых линий магнитного поля (заостренный полюс магнита). В случае перпендикулярной ориентации магнитик вообще никуда не отклонится и попадет в центр экрана.

Пропуская электроны мы будем наблюдать только отклонение вверх или вниз на одно и то же расстояние. Это пример квантования (дискретности). Спин электрона может принимать только одно из двух значений относительно заданной оси ориентации магнита – «вверх» или «вниз». Поскольку электрон мысленно представить себе нельзя (у него нет ни цвета, ни формы, ни даже траектории движения), как и во всех подобных анимациях цветные шарики не отражают реальность, но суть думаю понятна.

Если электрон отклонился вверх, то говорят, что его спин направлен «вверх» (+1/2 условно обозначают) относительно оси магнита. Если вниз, то -1/2. И казалось бы спин можно описать обычным вектором, указывающим направление. У тех электронов, где он был направлен вверх, они и отклонятся вверх в магнитном поле, а у которых вниз – те соответственно вниз. Но не все так просто! Электрон отклоняется вверх (вниз) на одно и тоже расстояние относительно любой ориентации магнита. На видео выше можно было бы менять не ориентацию пропускаемых магнитиков, а поворачивать сам магнит, создающий магнитное поле. Эффект в случае обычных магнитиков был бы тот же. Что будет в случае электронов – в отличие от магнитиков они всегда будут отклонятся на одно и тоже расстояние вверх или вниз.

Если, например, пропустить вертикально расположенный классический магнитик через два перпендикулярно ориентированных друг относительно друга магнита, то отклоняясь вверх в первом, он не отклонится во втором вообще никак – его вектор магнитного момента будет перпендикулярен линиям магнитного поля. На видео выше это тот случай когда магнитик попадает в центр экрана. Электрон же обязан куда-нибудь отклонится.

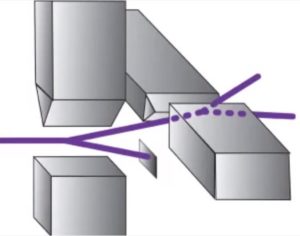
Если мы будем пропускать через второй магнит только электроны со спином вверх, как на рисунке, то окажется что часть из них оказались еще и со спином вверх (вниз) относительно другой перпендикулярной оси. Вправо и влево фактически, но спин измеряют относительно выбранной оси, поэтому «вверх» и «вниз» общепринятая терминология вместе с указанием оси. Вектор не может быть направлен сразу вверх и вправо. Делаем вывод, что спин – это не классический вектор, прикрепленный к электрону наподобие вектора магнитного момента магнитика. Более того, зная, что спин электрона направлен вверх после прохождения первого магнита (отклоняющиеся вниз блокируем), невозможно предсказать куда он отклонится во втором случае: вправо или влево.

Ну и можно еще чуть-чуть усложнить эксперимент – блокировать электроны, отклонившиеся влево и пропустить через третий магнит, ориентированный как и первый.

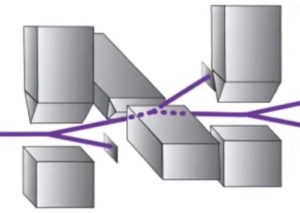
И мы увидим, что электроны будут отклонятся как вверх, так и вниз. То есть электроны, попадающие во второй магнит все имели спин вверх относительно ориентации первого магнита, а потом часть из них стала вдруг со спином вниз относительно той же самой оси.

Странно! Если через такую конструкцию пропускать классические магнитики, повернутые под одним и тем же произвольно выбранным углом, то они всегда будут попадать в конце в одну и ту же точку экрана. Это называется детерминизмом. Повторив эксперимент при полном соответствии начальных условий мы должны получить тот же результат. В этом заключается основа предсказательной силы науки. Даже наша интуиция основана на повторяемости результатов в схожих ситуациях. В квантовой механике предсказать куда отклонится конкретно взятый электрон в общем случае невозможно. Хотя в некоторых ситуациях есть исключения: если поставить два магнита с одинаковой ориентацией, то если электрон отклонится вверх в первом, то он точно отклонится вверх и во втором. А если магниты повернуты на 180 градусов друг относительно друга и в первом электрон отклонился, например, вниз, то во втором он точно отклонится вверх. И наоборот. Сам по себе спин не меняется. Это уже хорошо)

Какие из всего этого можно сделать общие выводы.

1. Многие величины, которые могли принимать любые значения в классической механике, могут иметь только некоторые дискретные (квантованные) значения в квантовой теории. Помимо спина энергия электронов в атомах является ярким примером.
2. Объектам микромира нельзя приписать никакие классические характеристики до момента измерения. Нельзя полагать, что спин имел какое-то определенное направление до того как мы посмотрели куда отклонился электрон. Это общее положение и оно касается всех измеряемых величин: координат, скорости и т.п. Квантовая механика субъективна. Она утверждает, что объективный, не зависимый ни от кого классический мир, просто не существует.  Теорема Белла наиболее наглядно демонстрирует данный факт. Роль субъекта (наблюдателя) в квантовой механике чрезвычайно важна.
3. Процесс измерения затирает (делает неактуальной) информацию о предыдущем измерении. Если спин оказался направлен вверх относительно оси y, то неважно, что раньше он был направлен вверх относительно оси x, он может оказаться и спином вниз относительно той же самой оси x впоследствии. Опять же данное обстоятельство касается не только спина. Например, если электрон обнаружен в точке с координатами (x, y, z) это в общем случае не значит, что он был в этой точке до этого. Данный факт известен под названием «коллапс волновой функции».
4. Есть такие физические величины значения которых невозможно знать одновременно. Например, нельзя измерить спин относительно оси x и одновременно относительно перпендикулярной ей оси y. Если мы попытаемся сделать это одновременно, то магнитные поля двух повернутых магнитов наложатся и мы вместо двух разных осей получим одну новую и измерим спин относительно нее. Последовательно измерять тоже не удастся вследствие предыдуще изложенного вывода №3. Это тоже общий принцип. Например, координату и импульс (скорость) тоже нельзя измерить одновременно с большой точностью — знаменитый принцип неопределенности Гейзенберга.
5. Предсказать результат единичного измерения невозможно в принципе. Квантовая механика позволяет лишь вычислять вероятности того или иного события. Например, можно посчитать, что в опыте на первой картинке при ориентации магнитов 90° друг к другу 50% отклонится влево и 50% вправо. Предсказать куда отклонится конкретно взятый электрон нельзя. Данное общее обстоятельство известно как «правило Борна» и является центральным в Копенгагенской интерпретации.
6. Детерминированные классические законы выводятся из вероятностных квантовомеханических за счет того, что в макроскопическом объекте очень много частиц и вероятностные флуктуации усредняются. Например, если в опыте на первой картинке пропускать вертикально ориентированный классический магнитик, то 50% составляющих его частиц будут «тянуть» его вправо, а 50% влево. В итоге он никуда не отклонится. При других ориентациях углов магнита меняется процентное соотношение, что в итоге и влияет на отклоняемое расстояние. Квантовая механика позволяет рассчитать конкретные вероятности и как следствие из нее можно вывести формулу для отклоняемого расстояния в зависимости от угла ориентации магнитика, получаемую обычно из классической электродинамики. Так классическая физика выводится и является следствием квантовой.

Да, описанные действия с магнитиками называются эксперимент Штерна-Герлаха.

Существует видеоверсия данного поста в части 2  и части 3 элементарного введения в квантовую механику.

Вторая статья цикла про спин электрона: Электроны в магнитном поле.

Все теперь в телеграм: https://t.me/lightcone_qm