Копенгагенская интерпретация квантовой механики

Квантовая механика настолько неинтуитивна, что было придумано несколько «интерпретаций» в терминах более доступных нашему мозгу для визуализации. Классической является «Копенгагенская интерпретация», переданная нам отцами-основателями: Вернер Гейзенберг, Вольфганг Паули, Пол Дирак, Нильс Бор и др.

Основные идеи Копенгагенской интерпретации довольно просты, но в то же время абстрактны:

1. Волновая функция (вектор состояния) следует унитарной эволюции во времени, описываемой уравнением Шредингера.
2. Физическим смыслом волновой функции является амплитуда вероятности, квадрат которой есть вероятность обнаружить систему при измерении в определенном состоянии. При измерении функция «коллапсирует», то есть сосредотачивается в точке, соответствующей результату измерения. Вся остальная информация об исходной функции теряется.

На счет первого пункта споров не идет. Унитарная эволюция является самым незыблемым фундаментальным физическим принципом на данный момент от которого в ближайшее время отказываться не собираются. Но вот по поводу второго пункта разногласия до сих пор не утихают. Отчасти потому что пункт 2 противоречит пункту 1. Коллапс волновой функции не является унитарной операцией! Он не подчиняется уравнению Шредингера. Казалось бы парадокс и несогласованность самой квантовой теории налицо.

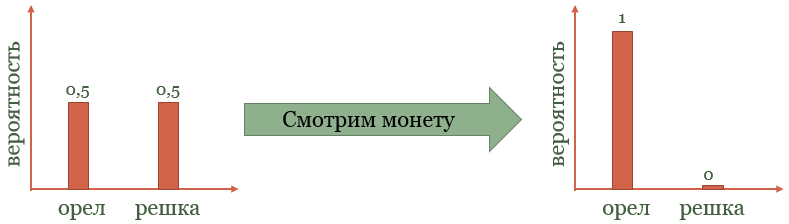
Тут есть один тонкий момент. Как нам показали отцы-основатели, роль наблюдателя в квантовой механике чрезвычайно важна. Квантовая механика субъективна. Все свои предсказания она выдает относительно наблюдателя — того субъекта кто ее использует. Экспериментатора. Тебя и меня. Поясним на примере. Представьте, что вы подкинули монетку и сейчас собираетесь посмотреть результат.

До того как вы подняли руку, результат можно оценить только с помощью распределения вероятностей. Если монета честная, то с вероятностью 50% выпадет орел и с 50% решка. Это все, что вы можете в данный момент сказать о системе. Но как только вы подняли руку и увидели результат — распределение вероятностей «коллапсирует» в одну точку — в тот результат который действительно выпал. То есть сейчас вы со 100% вероятностью можете сказать, что выпал орел.

Данный «коллапс» справедлив и для более сложных распределений вероятностей. Например, если подбрасывать два игральных кубика и смотреть вероятность выпадения того или иного числа (суммы выпавшего на первом и втором кубике — от 2 до 12), получим Гауссово распределение (выпадение семерки наиболее вероятно). Но когда мы реально смотрим на то что выпало в конкретном случае — это распределение коллапсирует в фактический результат (скажем в сумме выпало число шесть).

Квантовую механику можно рассматривать как обобщение теории вероятностей по аналогии с тем как комплексные числа являются обобщением действительных. Волновая функция условно является неким «квадратным корнем» из функции распределения вероятности. Для того чтобы найти вероятность — волновую функцию необходимо возвести в квадрат. Кроме того она комплекснозначная. Амплитуда вероятности в общем случае является комплексным числом. В остальном идея «коллапса» как получение новых знаний о системе и неактуальности предыдущей информации остается такой же.

Возьмем кубит, находящийся в квантовой суперпозиции:

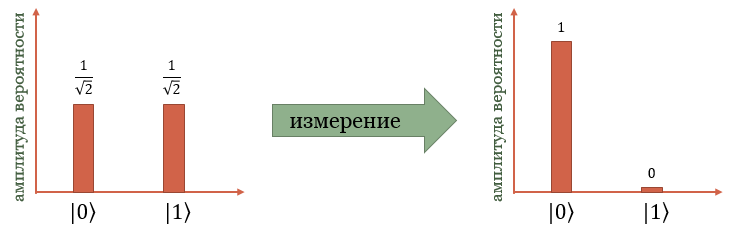
\( \displaystyle |\psi\rangle=\frac{1}{\sqrt{2}}|0\rangle+\frac{1}{\sqrt{2}}|1\rangle\)

При измерении происходит коллапс вектора состояния и мы получаем только одно из двух слагаемых. Либо при измерении мы получили ноль и вектор состояния коллапсирует в \( \displaystyle |\psi\rangle\rightarrow |0\rangle\), либо единицу и вектор переходит в \( \displaystyle |\psi\rangle\rightarrow |1\rangle\).

Отличие от классической теории вероятностей заключается еще и в том, что с монеткой мы подсознательно знаем, что она уже лежит или орлом или решкой до того как мы подняли руку чтобы посмотреть на результат. В случае квантовых объектов такое предполагать нельзя. Система приобретает классические свойства (характеристики) именно в момент субъективного измерения. Нельзя предполагать, что кубит до измерения был в состоянии \( \displaystyle |0\rangle\) или \( \displaystyle |1\rangle\). Он был именно в суперпозиции. Но эта суперпозиция ненаблюдаема. Поэтому слово был можно применять лишь условно. Вектор состояния не является объективной реальностью, как не является ею функция распределения вероятностей в классическом случае.

В этом и состоит разрешение парадокса кота Шредингера и других так называемых «парадоксов» в рамках Копенгагенской интерпретации — кот не является живым плюс мертвым. Это все равно что сказать: орел плюс решка, интерпретируя приведенную выше функцию распределения.

Кот или жив или мертв. Мы ничего более не обнаружим при измерении. Просто квантовыя механика запрещает нам неявно делать какие-либо выводы до фактического измерения и описывает систему суперпозицией. То что нельзя измерить — не существует. То что можно измерить, но еще не измерено тоже не существует объективно.

Запутанные состояния, так волновавшие Эйнштейна, также интерпретируются с вероятностных позиций как квантовые корреляции. Пусть система из двух спинов находится в синглетном состоянии:

\( \displaystyle |S\rangle=\frac{1}{\sqrt{2}}(|\uparrow\downarrow\rangle-|\downarrow\uparrow\rangle)\)

При измерении мы всегда обнаружим корреляции: если спин одной частицы направлен вверх относительно какой-либо оси, то спин второй частицы обязательно окажется направленным вниз относительно той же оси. И наоборот. Можно опять провести аналогию с классической теорией вероятностей. Возьмем красную и синюю таблетки. Перемешаем их у себя за спиной и зажмем в каждый кулак по штуке. Не разжимая руки мы не можем сказать где находится синяя,  а где красная. Можно построить график распределения вероятности аналогичный приведенному для монетки.

Но как только мы откроем один кулак и увидим, что там, например, синяя — мы мгновенно узнаем, что в другом кулаке красная. И наоборот. Это получение информации коллапсирует приведенный выше вектор состояния в одно из слагаемых. Таблетки могут быть разнесены на разные концы Вселенной и все равно статистические корреляции сохранятся. Очевидно, что тут не идет речь о сверхсветовой скорости передачи информации, простые корреляции.

Единственно новой вещью в квантовомеханическом случае является невозможность предположить, что в правой руке была синяя, а в левой красная до измерения. Теорема Белла или Загадка квантовых пирожков наиболее наглядно это разъясняют. Именно измерение данным наблюдателем какого-либо свойства (цвета в нашем случае) делает его реальным (объективным) для этого наблюдателя.

Квантовая механика субъективна. Она дает предсказания только для того кто ей пользуется. Только для него происходит субъективный коллапс вектора состояния, связанный с получением новой информации. Объективный мир существует только в его голове. Для всех других он такая же часть физического мира и подчиняется тем же самым квантовомеханическим законам с суперпозициями, комплексными числами и тому подобными вещами. Друг Вигнера является наглядной демонстрацией данного принципа.

Волновая функция (вектор состояния) ненаблюдаема. Это не классическое поле типа температуры или напряженности электрического поля. Эта функция скорее ближе к функции распределения вероятности, точнее ее можно рассматривать как некое ее обобщение. Саму квантовую механику можно рассматривать как обобщение теории информации + теории верояностей.