A surge of attacks against classical GR
Luboš Motl, September 29, 2014
A decade ago, an organized movement of hardcore crackpots began its public assaults against string theory.
Because most of the central results of the string theory paradigm have been established with as much rigor as you may ever get in natural science, it was pretty clear to me that given someone’s semi-successful efforts to obfuscate some of the pillars of state-of-the-art science, it would soon or later become possible to attack any result in science and team up with journalists who will do the job.
The deterioration of the public discourse was faster than I could imagine. To quantify some of these processes, note that the resistance to string theory requires one to reject some of the most important results of science of the 1990s and sometimes the 1980s. You could say that they’re still «recent enough» so that the people interested in science haven’t had enough time to absorb them yet – 20 or 30 years may be considered «too short a period».
However, what we saw later was the escalating questioning of the very basic postulates of quantum mechanics which is really a framework of modern physics almost fully uncovered in the 1920s. That’s almost 90 years ago. We have been seeing totally idiotic articles about the foundations of quantum mechanics in the media that call themselves «science media», pretty much on a daily basis.
Well, even 90 years isn’t enough, it seems, so right now, we are entering new waters – the denial of some basic results of general relativity, our modern theory of gravity that has been around and available to everyone since 1916. So in the last week, hundreds of publications informed their readers that it’s been «mathematically proven» that the big bang theory is wrong and the black holes don’t exist.
These nutty claims boil down to some papers by a crackpot named Ms Laura Mersini-Houghton (no, I really, really won’t accept her doctorate) who had previously claimed that she could see an opening of a wormhole leading to another Universe in some cold spots in the CMB (which aren’t that cold at all, and even if they were, the interpretation was totally silly).
She wrote some totally idiotic preprints claiming that the Hawking radiation prevents a star from forming a black hole. It’s just a staggeringly stupid claim. For a stellar size black hole (by the mass), it takes something like \(10^{100}\) years for it to evaporate via the Hawking radiation. On the other hand, the collapse time may be comparable to seconds, a very short timescale, so be sure that almost nothing changes about the distribution of matter thanks to the Hawking radiation even if you could exactly define what you consider to be the Hawking radiation in this short, initial, out-of-equilibrium phase.
While this crank got exactly the same treatment in the media as Albert Einstein in the New York Times after Eddington’s 1919 expedition has confirmed the bending of light predicted by the 1916 GR, I don’t want to discuss this any further because if someone is incapable of producing some right arguments why the claim is preposterous, he won’t understand the explanations by someone else, anyway. If someone thinks that he understands some science but he is willing to change his opinion about the very existence of black holes right after he or she reads some inkspiller’s rant in the newspapers, he is a dangerous lunatic and I don’t want to interact with such a dangerous lunatic without a firearm in my hands.
But Mersini-Houghton’s papers aren’t quite unique. You may find several if not numerous similar super-idiotic papers claiming that the black holes don’t exist etc. Just to be sure, I don’t really count the «firewalls exist» paper to this super-idiotic category because while all of these papers are ultimately and inevitably wrong, they built on arguments rooted in quantum gravity – quantum information studied in the context of black holes – which may be considered hard as well as «primary» in the sense of «being able to negate conclusions of classical GR».
However, the super-idiotic papers really deny some of the most elementary results of classical general relativity in contexts where classical general relativity obviously applies. One of such deeply embarrassing, super-idiotic papers was recently co-authored by Lawrence Krauss.
Is there a simple insight or observation that may be mentioned to quickly kill all such papers? Is there some basic misconception that all these super-idiotic papers and their advocates share, before they please us with all the amazing conclusions that the black holes don’t exist, stars don’t collapse, Hawking radiation is incompatible with horizons, and so on?
I remember that when I was a kid who knew Einstein’s equations but didn’t quite know what is implied by their application, I was confused about some points that may be a candidate to answer the question in the previous sentence. The problem is a distrust in Penrose’s causal diagrams, especially in some of their counterintuitive features such as the «breakdown of the time-translational symmetry» of a black hole solution. A previous blog post was explaining why objects may fall beneath the black hole horizon and why the interior exists as a consequence. But if someone understands how to deduce a Penrose diagram, why the derivation is OK and qualitatively unique, and why it has consequences for the question «what is possible in a spacetime», he must be able to sort all these things by himself.
OK, when people talk about the black hole, they want to think about the oldest 4D example (whether it’s really the «simplest one» is a matter of perspective, however), the Schwarzschild neutral black hole solution
\[
{d \tau}^{2} = \left(1 — \frac{r_s}{r} \right) dt^2 — \frac{dr^2}{1-r_s/r}-
r^2 \left(d\theta^2 + \sin^2\theta \, d\varphi^2\right),
\]
\[ r_s = \frac{2GM}{c^2} \]
Note that the metric tensor components don’t depend on the time coordinate \(t\) at all so the solution is «static» in these (and some other) coordinates. In these coordinates, the infalling observer «never» reaches the event horizon because his convergence towards \(r=r_s\) is being slowed down and so on.
However, it’s clear that if you approach the \(r=r_s+\epsilon\) region, the numerical values of the metric tensor in these coordinates become singular and you must make a «significantly» nonlinear coordinate transformation to make the region look like the ordinary Minkowski space in ordinary coordinates. And be sure it’s possible to do so. Because all the curvature invariants are very low if the black hole is large, the region right above the event horizon is a nearly flat, Minkowskian pieces of a spacetime. And there must exist better coordinates in which the metric tensor is less singular.
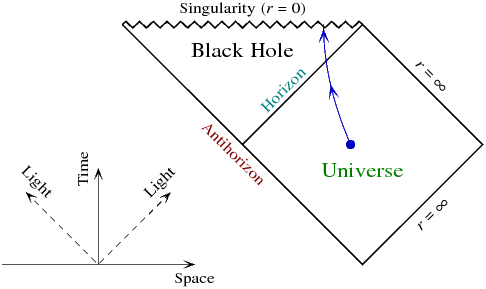
Now, there is a mathematical exercise everyone should be able to follow. Any good enough, modern textbook on GR contains this explanation. If you master this exercise or at least follow the derivation, you will see that the right coordinates that are non-singular near the event horizon may be continued beneath the horizon and the whole spacetime – which is effectively 2-dimensional because the geometry only depends on the angular variables \(\theta,\phi\) in a trivial way – looks like the Penrose diagram above.
I usually like to draw the piece at the top expressing the Hawking radiation but I decided to post the classical GR diagram this time because this blog post is really about classical GR although some people like to obfuscate this fact, too.
The Penrose diagram makes it totally clear that there exists a totally smooth region of the spacetime we may call the black hole interior and an observer may get there – and under certain circumstances, he inevitably ends up there.
A key and potentially confusing property of the Penrose diagram is that the manifest time-translational symmetry of the original Schwarzschild solution in the Schwarzschild coordinates is lost, broken, violated, refuted. If the time-translational symmetry were there, you could think that the Penrose diagram will be just «some picture» copied all over the vertical axis – that the picture wouldn’t depend on the \(y\)-axis at all. But the actual Penrose diagram does depend on the \(y\)-coordinate.
This conclusion is simply a fact. If you want to study phenomena near the horizon and especially inside the horizon and recognize that the people experiencing these phenomena locally feel a piece of nearly flat, ordinary, Minkowskian spacetime, you simply have to use coordinates in which the time-translational symmetry of the Schwarzschild solution is non-manifest. You can’t see it and it doesn’t have any local consequences. One could say that the time-translational symmetry is «morally broken» for all these phenomena near (and especially beneath) the event horizon.
General relativity makes this conclusion inevitable. The theory has the right to lead to similar conclusions and it uses the right efficiently. After all, this conclusion about the «effectively broken time-translational symmetry of a black hole» shouldn’t be surprising. It is not the only case in which GR makes the «naive static or stationary» description one could believe at the beginning impossible. When we ask GR whether the distances between galaxies in an otherwise uniform cosmos may be constant, the answer is
No, they must evolve just like the distance between the Earth and a free-falling apple, so the cosmos either has to expand or shrink at almost all times.
Indeed, this is how the big bang theory follows from GR. Needless to say, the ingenious crank Ms Laura Mersini-Houghton has disproved the big bang theory, too, so my explanation that the two situations are analogous is no useful because she reached the wrong answers about both situations. 😉
If we return to the case of the black hole, we may mention other reasons why it was inevitable for the Penrose diagram to destroy the manifest time-translational symmetry. Why? Well, it’s because the slices \(t={\rm const}\) in the original Schwarzschild geometry are 3-dimensional space-like slices for \(r\gt r_s\). But if you investigate how the 3-dimensional manifolds given by \(t={\rm const}\) look for \(r\lt r_s\), you will notice that the coordinate \(r\) itself becomes time-like – the component \(g_{rr}\) of the metric tensor reverts the sign. That’s why \(t={\rm const}\) cannot be interpreted as «one moment» from the viewpoint of any finite-speed observer who is already inside the black hole. It follows that decent, non-singular coordinate systems that observers inside the black hole may use are simply not allowed to use \(t\) as one of the four coordinates. Because «constancy in \(t\)» was how the static character of the solution manifested itself and because \(t\) is no longer one of the four coordinates we use, it’s clear that the static nature of the solution (the Killing vector) will no longer be manifest.
Another way to express a similar idea is to notice that even in the Schwarzschild coordinates, the \(r=r_s\) locus is null – the proper distances in the direction where \(t\) increases while the remaining coordinates are fixed is zero. It’s because \(g_{tt}=0\) for \(r=r_s\). So this manifold, if it is 3-dimensional at all, must look like a null (i.e. by 45 degrees tilted) hypersurface in «decently non-singular coordinates», so it cannot be vertical! Much like in the big bang case, the right Penrose diagram must make the black hole interior look like either expanding or shrinking beast. Again, it chooses the former (expanding; the shrinking picture would describe a «white hole», a time-reversal image of the black hole, which is forbidden by the second law).
The formation of the event horizon is inevitable and can’t be affected by tiny perturbations such as the «Hawking radiation already emerging during the star collapse». When you are standing on the surface of a collapsing star, you suddenly feel that you’re falling towards the center. At some moment, you cross the event horizon but from your viewpoint, this moment doesn’t differ from other moments at all. The point is that the precise location of the horizon is a quantity that may only be determined once we know the full future evolution as well: the interior (the region beneath the event horizon) is the region from which one can’t escape in the future, so whether you may escape from your current location depends on the evolution in the future, too.
On the other hand, you see that the interior of the black hole approaches the singularity, and this evolution is inevitable, too. It can’t be stopped from outside. Why? Look at the first point of the singularity (the horizontal line with teeth) on its left end. And perhaps a millimeter around that point of the Penrose diagram. If something affects this small region, it must be an event that is in the causal past. But all such points belong to the «antihorizon» (or its vicinity) and the «antihorizon» only contains events before the star began to collapse which can no longer be changed because the history can’t be rewritten anymore; or events inside the black hole – which are are also determined by the object that collapsed. So the increasing curvature etc. is really inevitable and the singularity has to form if Einstein’s equations hold (even if they hold up to small corrections) – a point made very rigorous by the Penrose-Hawking and other singularity theorems.
Numerous people are just unfamiliar with this basic material and they write insanely wrong papers.
But more generally, I want to say that an intelligent reader of the newspapers just can’t take these constant reports about the permanent counterrevolution in physics seriously – even for reasons that must be comprehensible to a science-illiterate person such as a historian.
New insights that get really established after they are described in well-known and particular papers by legitimate scientists simply never go away after decades of their reign. And even if something fundamental about science gets reverted, these are extremely rare, once-per-century events. In the 20th century, we saw the rise of special relativity, general relativity, quantum mechanics, quantum field theory, string theory, and perhaps several other comparable advances in physics.
Changes that are this dramatic occur several times per century – and the percentage of such rare discoveries that moreover claim that some other key discovery from the last 100 or 200 years is completely wrong is even lower. So such an advance that would fully negate a 100-year-old fundamental discovery is an extremely rare event. It may perhaps take place once in 300 years.
So if your newspapers bring you a report every week (if not every day) that someone has made exactly such a discovery refuting string theory or quantum mechanics or general relativity or the existence of black holes or the uncertainty principle etc. and if you have at least some common sense left, you may be sure that the percentage of reports in your newspapers that are «complete bullšit» is close to
\[ 100\% \left( 1 — \frac{1}{52\times 300} \right) = 99.994\%\]
Do you agree that if 99.994% of some reports in a news outlet is complete rubbish, this news outlet has nothing whatever to do with the real world and no sane person should take it seriously? You should agree, indeed. Needless to say, the percentage is an optimistic underestimate. In reality, similar newspapers almost never report the actual important advances in science. They are just way too occupied by presenting complete rubbish as revolutions in science.


