Квантовые компьютеры. Алгоритм Дойча.

Логика квантовой механики отличается от классической логики теории множеств которой мы пользуемся повседневно (см. загадку квантовых пирожков или теорему Белла). Квантовые компьютеры принципиально отличаются от классических именно логикой работы, а не просто переходом от транзисторов к чему-то наноразмерному.

Классический бит заменяется квантовым битом — кубитом, вектор состояния которого может принимать значение ноль:
\( \displaystyle |\psi\rangle=|0\rangle\)
Может принимать значение единица:
\( \displaystyle |\psi\rangle=|1\rangle\)
А может содержать любую их комбинацию (суперпозицию):
\( \displaystyle |\psi\rangle=c_{0}|0\rangle+c_{1}|1\rangle\)
где \( \displaystyle c_{0}\) и \( \displaystyle c_{1}\) — комплексные числа, называемые амплитудами вероятности.

Сама суперпозиция ненаблюдаема. При измерении кубита мы всегда обнаружим либо ноль с вероятностью   \( \displaystyle |c_{0}|^{2}\), либо единицу с вероятностью  \( \displaystyle |c_{1}|^{2}\).

Над кубитом можно производить некие (унитарные) операции, которые изменяют численные значения коэффициентов \( \displaystyle c_{0}\) и \( \displaystyle c_{1}\).

Как работает квантовый компьютер можно понять на примере простейшего квантового алгоритма Дойча. Предположим у нас есть черный ящик, который вычисляет некую булеву функцию \( \displaystyle f(x)\) одной переменной.

На вход мы можем подать либо ноль, либо единицу, и на выходе получим ноль или один. Всего возможны четыре варианта таких функций. Их можно разделить на две категории: константные и сбалансированные.

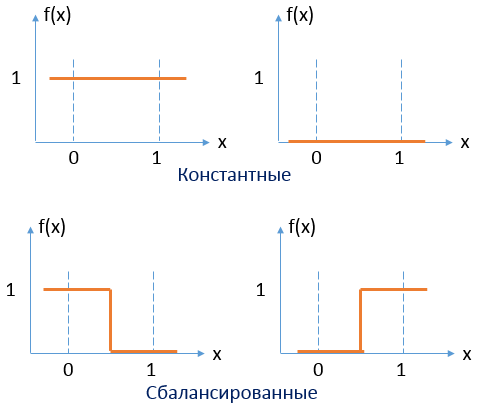
Стоит задача (задача Дойча): определить к какой из этих двух категорий относится функция в черном ящике.

Единственной возможностью решить данную задачу на классическом компьютере является подача на вход сначала нуля, а потом единицы. То есть функция \( \displaystyle f(x)\) вызывается два раза. Фактически после этого мы однозначно определим вид функции, а не только категорию. Однако определить категорию за один вызов функции на классическом компьютере не удастся, в отличие от квантового.

Интуитивно становится понятно, что произойдет в квантовом случае, ведь кубит содержит суперпозицию нуля и единицы. Возьмем кубит вида:
\( \displaystyle |\psi\rangle=\frac{1}{\sqrt{2}}|0\rangle+\frac{1}{\sqrt{2}}|1\rangle\)
то есть коэффициенты \( \displaystyle c_{0}=c_{1}=\frac{1}{\sqrt{2}}\) и вероятность при измерении кубита получить единицу равна вероятности получить ноль и равна 50% поскольку \( \displaystyle \left | \frac{1}{\sqrt{2}}\right|^{2}=0.5\). Подадим его на вход следующей схемы.

Операция F изменяет коэффициенты \( \displaystyle c_{0},c_{1}\)  кубита следующим образом:

\( \displaystyle |\psi\rangle=\left [\frac{1}{\sqrt{2}}(-1)^{f(0)}\right ]|0\rangle+\left [\frac{1}{\sqrt{2}}(-1)^{f(1)}\right ]|1\rangle\)

По сути F есть квантовомеханический аналог классического черного ящика f. Заметьте, что измерив кубит сразу за блоком F вне зависимости от вида функции \( \displaystyle f(x)\)  мы продолжим получать 50%-ю вероятность нуля и единицы, поскольку она может изменить только знак, а  \( \displaystyle \left | \frac{1}{\sqrt{2}}\right|^{2}=\left | \frac{-1}{\sqrt{2}}\right|^{2}=0.5\).

Применяя к кубиту преобразование Адамара H, мы опять меняем амплитуды вероятностей и получаем:

\( \displaystyle |\psi\rangle=\frac{1}{2}\left [(-1)^{f(0)}+(-1)^{f(1)}\right ]|0\rangle\) \( \displaystyle +\frac{1}{2}\left [(-1)^{f(0)}-(-1)^{f(1)}\right ]|1\rangle\)

Теперь можно измерять кубит последним блоком. Убедитесь, что для константных функций мы получим \( \displaystyle c_{0}=1,c_{1}=0\), а для сбалансированных наоборот \( \displaystyle c_{0}=0,c_{1}=1\). То есть если в результате измерения будет ноль — функция константная, если единица — сбалансированная.

Заметьте, что в отличие от классического случая, операция F выполнялась только один раз (на квантовом компьютере)), но мы можем однозначно сказать к какой категории относится функция (хотя ее конкретный вид остается неясным). Это пример так называемого квантового параллелизма. Теоретически мы можем получить экспоненциальный рост производительности при линейном росте количества кубит. Для описания двухкубитного состояния требуется уже четыре комплексных числа \( \displaystyle c_{00}…c_{11}\):

\( \displaystyle |\psi\rangle=c_{00}|00\rangle+c_{01}|01\rangle+c_{10}|10\rangle+c_{11}|11\rangle\),

а для N-кубитного \( \displaystyle 2^{N}\) чисел, то есть имеет место экспоненциальный рост.

Квантовые вентили оперируют всем вектором состояния, который содержит суперпозицию всех возможных классических бит за счет чего и реализуется квантовый параллелизм. Однако, как мы видели на примере, чтобы считать результат необходимо чтобы все кроме одной амплитуды вероятности обратились в ноль. Только в этом случае возможно получить четкий ответ на поставленную перед алгоритмом задачу. В большинстве же случаев это не удается и ответ носит вероятностный характер который приходится проверять классическим компьютером. Из-за этих ограничений квантовые алгоритмы пока получают применение в основном только для весьма специфических задач где встречаются однонаправленные функции.

Например, легко перемножить два числа, но разложить число на сомножители уже сложно. Квантовый алгоритм Шора выдает, скажем с 80%-й вероятностью, что делителем является число 464533434. Но его необходимо проверить классическим компьютером. Благо проверить делится ли одно число на другое несравнимо быстрее, чем искать делители.
Задачу поиска также можно отнести к рассматриваемой категории задач: легко проверить на этой ли позиции находится искомый элемент, но перебирать весь массив долго. Квантовый алгоритм Гровера, решающий задачу перебора, дает квадратичное ускорение по сравнению с классическими.

Вся несимметричная криптография основана на таких функциях: контрольная сумма, электронная подпись, хэш. Области применения сейчас очень широкие — банковские транзакции, криптовалюта, защита каналов связи и др. Все это становится легко взламываемым с появлением квантовых компьютеров.

Практическая реализация квантовых компьютеров тормозится сложностью масштабирования. Мы видели, что система из N кубит описывается одним вектором состояния. То есть кубиты не являются независимыми как обычные биты. Скорее увеличение количества кубит похоже на увеличение разрядности регистров классических процессоров.

Если физическую реализацию однокубитного состояния найти довольно просто (спин электрона, поляризация фотона), то для двухкубитного нужны комбинированные системы типа электронов или фотонов в запутанном состоянии. Создать и поддерживать многокубитную систему достаточно сложно поскольку взаимодействие с окружающей средой и подсистем между собой изменяет исходный вектор состояния. Поэтому в качестве физического носителя необходимо использовать то, что относительно слабо взаимодействует с внешним миром, например, фотоны. Либо минимизировать воздействие самой окружающей среды: криогенные температуры, экранирование и т.п.