Карусель Эйнштейна

Проанализируем что происходит на известном советском аттракционе «Сюрприз» с точки зрения теории относительности.

Движение по кругу даже с постоянной скоростью вращения, как ни странно, это движение с ускорением. Скорость является векторной величиной. При движении по кругу с постоянной угловой скоростью не меняется длина вектора v, но постоянно меняется его направление.

То есть три декартовы компоненты скорости \( \displaystyle v_{x},v_{y},v_{z}\) все время меняются, оставляя неизменной длину \( \displaystyle |v|=\sqrt{v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}\). Ускорение также является векторной величиной и определяется как производная от скорости. В нашем случае меняющейся скорости оно не будет нулевым. Именно его и ощущают участники аттракциона в виде центробежной силы, прижимающей их к стенке.

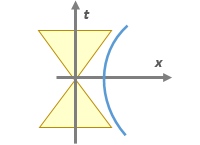
С точки зрения стороннего наблюдателя в каждый момент времени участнику аттракциона можно приписать линейную скорость движения v — тот самый касательный вектор на рисунке. Соответственно, с его точки зрения будут наблюдаться все эффекты специальной теории относительности. Если людям на карусели дать линейки, то их длины будут сокращаться. Если им дать часы, то они будут идти медленнее.

Если маленькими линейками замостить всю окружность, то мы придем к выводу, что при вращении сама длина окружности сокращается на релятивистский фактор \( \displaystyle \sqrt{1-v^2/c^2}\). Диаметр окружности при этом останется неизменным поскольку Лоренцево сокращение происходит только по направлению движения, а диаметр измеряется перпендикулярно ему. Но ведь отношение длины окружности к диаметру всегда постоянно и равно числу пи. Возникает парадокс (парадокс Эренфеста).

Эренфест видел решение парадокса в отказе от понятия «абсолютно твердое тело». Он считал, что вращающийся диск должен деформироваться чтобы уменьшить свой радиус в соответствии с формулой \( \displaystyle l=2\pi r\).

Эйнштейн считал, что саму формулу необходимо модифицировать:

\( \displaystyle l=2\pi r\sqrt{1-v^2/c^2}\)

Точнее даже не формулу, а саму геометрию в рамках которой справедлива данная формула — Евклидову геометрию.

Поскольку согласно принципу эквивалентности ускоренное движение эквивалентно гравитации, данный мысленный эксперимент с каруселью показывает, что гравитационное поле также оказывает влияние на ход часов. Чем сильнее гравитационное поле, тем медленнее идут часы. Эйнштейну удалось получить этот нетривиальный результат даже в отсутствии окончательно сформулированной теории гравитации.