Математические открытия или изобретения? Связь математики с физикой.

Роль математики в физике сложно переоценить. Известна цитата Галилео Галилея «Математика — это язык, на котором написана книга Природы». Но только ли языком является современная математика? Работа математиков заключается в нахождении новых математических объектов и исследовании их свойств и взаимосвязей. Со времен Галилея появилось множество новых разделов математики со своим языком для описания математических объектов.

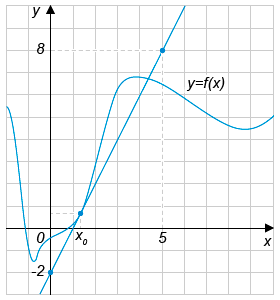
Возьмем известный всем математический объект — функцию. В школьной программе ее вводят в виде \( \displaystyle y=f(x)\) и подразумевают задание какой-то зависимости переменной y от переменной x.

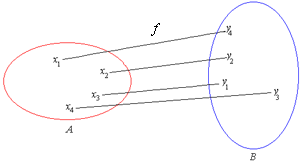
Однако с точки зрения теории множеств, функция — это отображение одного множества в другое:

\( \displaystyle A\overset{f}{\rightarrow}B \)

А с помощью абстрактной алгебры функцию можно представить в виде оператора, а набор значений x и y считать векторами. В данном описании задание функции эквивалентно заданию матрицы оператора \( \displaystyle \hat{F} \).
\( \displaystyle Y=\hat{F}X \)

А в теории возмущений, функции привычнее задавать в виде бесконечного ряда. Причем для разных областей определения функции конкретный вид ряда может отличаться.

\( \displaystyle f(x)=\sum_{n=0}^{\infty }a_{n}x^{n} \)

То есть функция существует как некий абстрактный математический объект, который можно «увидеть» с помощью разных математических методов. Данные рассуждения можно отнести практически к любому математическому объекту. Вектор, например, можно задать абстрактным символом \( \displaystyle \overline{v} \) или конкретным координатным представлением \( \displaystyle (v_{x},v_{y},v_{z}) \). Причем численные значения этих координат будут зависеть от выбранной системы координат и базиса.

Так существуют ли математические объекты, которых миллионы (или бесконечность?), как некие абстрактные сущности вне времени и пространства и которые в какой-то момент были просто открыты математиками и не зависят от конкретных способов описания/исследования? Или же все это изобретения человеческого ума?

Данный вопрос обсуждается еще со времен античных философов. Одни считают, что математические объекты существуют в «Платоновском мире идей» независимо от нас. Роджер Пенроуз — яркий представитель данного направления.

Вроде бы логично. Многие математические объекты были открыты независимо разными людьми и даже разными цивилизациями. Теорема Пифагора и другие аспекты Евклидовой геометрии или некоторые факты из теории чисел были известны всем древним культурам. Теорема Пифагора или натуральные числа в этом смысле существовали всегда в Платоновском мире. Позднее были открыты отрицательные числа, действительные числа, комплексные числа, кватернионы. Открываемые математические объекты становятся все более абстрактными: Грассмановы числа, группы, кольца, поля, расслоения… Но все они подчиняются тем или иным правилам, которые выполнялись всегда и будут выполняться всегда. Мало кто сомневается, что теорема Пифагора работала даже до формирования Земли и зарождения жизни. Евклидово пространство как математическая структура, таким образом, занимает свой уголок в Платоновском мире.

Однако существует противоположная точка зрения которую разделяют даже некоторые топовые математики, например, Майкл Атья.

Идея такова — в корне всех математических открытий все равно лежат наблюдения, полученные нами через органы чувств. Майкл говорит, что если бы мы не видели вокруг себя дискретных вещей (были бы плазмоидной формой жизни на планете типа «газовый гигант»)), то даже понятие числа и арифметика не были бы изобретены. Что не означает отсутствие математики вообще, просто она была бы другая.
Действительно, откройте современную статью по абстрактной алгебре и вы не увидите ни одного числа. Без органов зрения и соответствующей эволюции мозга не было бы пространственного воображения и геометрии в том виде, как мы ее знаем. И так далее, то есть математика — это изобретение человечества. Из бесконечного набора гипотетических математических объектов выбираются лишь некоторые, которые наш ограниченный мозг может осознать, и следовательно они (хоть и не всегда очевидно) связаны с окружающей реальностью. Микеланджело говорил «Скульптура уже существует внутри куска мрамора. Я лишь отсекаю лишнее». Так и математические объекты скорее создаются математиками подобно скульптуре из океана бесконечных возможностей.

В рамках этой парадигмы Майкл отвечает и на известный вопрос физиков, сформулированный в известной статье Ю.Вигнера Необъяснимая эффективность математики в естественных науках. Почему в современной теоретической физике находят применение такие абстрактные математические объекты, которые казалось бы не имеют никакого отношения к реальности. Атья говорит — математика в конечном счете, как и физика, основана на наблюдениях окружающего мира. Ничего удивительного, что она отражает реальность.

Работа физика-теоретика заключается в построении математической модели, которая бы описывала наблюдаемые явления и желательно предсказывала бы существование новых. Все физические теории — это математические модели. Закон Ньютона выражается математически как  \( \displaystyle F=ma \). Это на самом деле пример модели, основанной на дифференциальном уравнении, поскольку ускорение есть вторая производная по времени. То есть в развернутом виде закон Ньютона выглядит как:

\( \displaystyle m\frac{d^{2}x(t)}{dt^{2}}=F(x) \)

Для Ньютоновской механики необходимо дифференциальное исчисление. Для общей теории относительности Эйнштейна нужна уже неевклидова геометрия, точнее Риманова геометрия. Для квантовой механики абстрактная алгебра с Гильбертовыми пространствами и линейными операторами. Но в то же время нельзя оспорить, что математика имеет дело с куда большим диапазоном исследуемых абстрактных структур, чем физика. Математика ограничена лишь логикой. Она не ограничена, скажем, тремя пространственными измерениями или физическими принципами.

Куча теорем имеют только математическую ценность (пока?). Но часть из них служит основой физики. С этой точки зрения физика — всего лишь часть математики. Дополнительные физические принципы, не берущиеся обычно математиками в рассмотрение, жестко ограничивают выбор возможных математических структур для описания физических явлений. Современная физическая теория должна быть инвариантной относительно преобразований Лоренца и калибровочных преобразований, не противоречить постулатам квантовой механики и т.д. На самом деле это очень жесткие ограничения, но даже в рамках них существует множество пространства для маневров.

Крайняя точка зрения в этом направлении высказывается Максом Тегмарком — физического мира как такового не существует, мы находясь внутри математического мира и являясь его частью просто ощущаем его таковым. Задачей физики является нахождение «своих координат» в этом математическом мире, то есть поиск тех математических структур, которые позволяют развиться таким самоосознающим объектам типа нас с вами и наблюдаемой Вселенной с ее законами в целом.

Между тем, хотя физику и можно считать частью математики, она оказывает большое влияние на ход развития последней. Дифференциальное и интегральное исчисления были открыты Ньютоном в связи с задачами механики. И хотя обычно необходимая математика оказывается уже существующей к моменту становления новой физической теории (так было и с теорией относительности, и с квантовой механикой), современная физика оказывает влияние и на чистую математику.

Как только физика вышла за диапазоны величин непосредственно доступных органам чувств человека (скорости близкие к скорости света, атомарные расстояния и т.п.), оказалась востребована крайне абстрактная математика недоступная для визуализации нашим мозгом. Никто не может представить себе электрон, электромагнитную волну или четырехмерное пространство-время. Все что нам осталось — это исследовать описывающие их математические структуры. И чем детальнее описание, тем более абстрактные математические объекты возникают. И без подсказки Природы математики вряд ли додумались бы копать в сторону этих структур. Так появились квантовые группы, некоммутативная геометрия, твисторы и тому подобные вещи. Экспериментальная физика дает математике современную замену органам чувств.

Вопросы касательно объективного существования всегда уходят в сторону философии. Стоит ли отождествлять электрон с математической структурой для его описания? Единственно ли вообще математическое описание физического объекта или разные математические структуры могут описывать одну физику? Существует ли объективная реальность для любой математической структуры?
Девяносто девять процентов всех существовавших когда-либо на Земле биологических видов (по текущим оценкам 5 миллиардов) к настоящему моменту вымерли. Но они отличаются всего лишь структурой ДНК. В Платоновском мире это соседние области математического пространства. Существуют ли объективно эти вымершие или никогда не существовавшие в нашем мире животные в «параллельных вселенных»? Здесь опять прослеживается тесная связь с современной физикой. Многомировая интерпретация квантовой механики утверждает, что все возможные эволюционные траектории существуют объективно. Однако классическая, Копенгагенская интерпретация, говорит совсем противоположное — объективный мир вообще не существует. По крайней мере независимо от субъекта — наблюдателя.
Субъективна ли математика?

Более полная и академическая версия статьи: Антропность математики

Если дочитали до конца, поддержите автора!