Принцип эквивалентности
Знаменитый принцип эквивалентности позволил Эйнштейну перейти от специальной теории относительности, описывающей движение с точки зрения различных систем отсчета, к общей теории относительности, описывающей гравитацию. С первого взгляда гравитация не имеет никакого отношения к движению. Мы чувствуем гравитационное поле Земли даже находясь неподвижно на ее поверхности.
Мы ощущаем воздействие гравитационного поля через величину, называемую весом. Вставая на весы мы измеряем именно свой вес относительно гравитационного поля Земли. На других планетах вы бы увидели другие показания своего веса. В интернете полно таких калькуляторов. Сила, давящая на весы, обусловлена притяжением к Земле и вычисляется согласно закону всемирного тяготения Ньютона:
\( \displaystyle F=G\frac{mM}{r^2}\)
где m — масса тела на весах; М — масса Земли; r — расстояние от весов до центра Земли; G — гравитационная постоянная Ньютона.
Но эту силу можно имитировать, используя другой закон Ньютона:
\( \displaystyle F=ma\)То есть можно подобрать ускорение, чтобы получилась такая же величина силы. Приравняв друг другу эти силы получим:
\( \displaystyle ma=G\frac{mM}{r^2}\)Принцип эквивалентности гласит, что масса в левой части формулы (инерционная масса) является той же самой физической величиной m, стоящей в правой части (гравитационная масса). И, таким образом, их можно сократить, получив:
\( \displaystyle a=G\frac{M}{r^2}\)Оказывается движение с ускорением (левая часть) эквивалентно гравитации (правая часть). Для земной гравитации величина этого ускорения широко известна:
\( \displaystyle a\approx 9.8 м/с^{2}\)Его обычно обозначают буквой \( \displaystyle g\). При вертикальном взлете ракеты к этому \( \displaystyle g\) добавляется ускорение ракеты при наборе скорости. Космонавт испытывает перегрузки. При ускорении ракеты \( \displaystyle 9.8 м/с^{2}\) космонавт ощущает, что его вес увеличился в два раза (\( \displaystyle 2g\)).
Но вес можно и уменьшить вплоть до нуля. Это состояние называется невесомостью. И согласно принципу эквивалентности при этом даже нет необходимости убирать до нуля гравитационное поле. Его можно компенсировать движением с ускорением. Знаменитый мысленный эксперимент Эйнштейна «человек в лифте» поясняет идею.
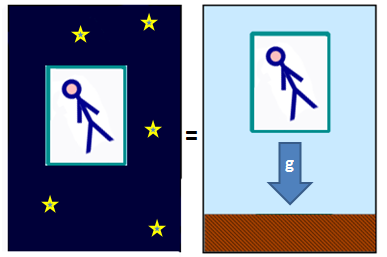
Человека запертого в шумонепронецаемом и непрозрачном лифте сбрасывают с самолета. Гравитационное поле заставляет его падать по направлению к земле с ускорением \( \displaystyle g\). Человек при этом ощущает состояние невесомости и не имея возможности посмотреть наружу не сможет сказать находится ли он в свободном падении в гравитационном поле или просто покоится в каком-нибудь месте в отсутствии гравитационного поля, где-нибудь в космосе вдали от звезд и планет.
Если же поместить этот лифт в ракету, движущуюся в космосе вдалеке от гравитирующих звезд с ускорением \( \displaystyle 9.8 м/с^{2}\), он не сможет отличить ситуацию от той, если бы лифт находился на поверхности земли.
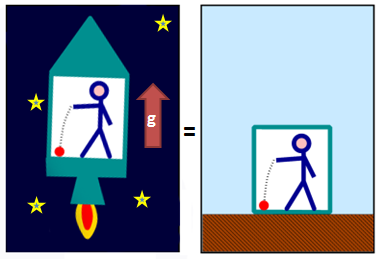
Сейчас состояния невесомости и перегрузки получают на коммерческой основе в самолете, который то набирает высоту с ускорением, то свободно падает вниз.
По той же причине космонавты на орбите испытывают невесомость. Она обусловлена не тем, что гравитационное поле вдруг стало равно нулю (оно практически такое же, что и на поверхности земли). Просто они постоянно падают на землю, но не достигают ее поверхности из-за огромной линейной скорости — первой космической скорости, компенсирующей приближение к поверхности земли. Траектория движения, обусловленная центростремительной силой притяжения и этой скоростью, как раз и будет окружностью или эллипсом.
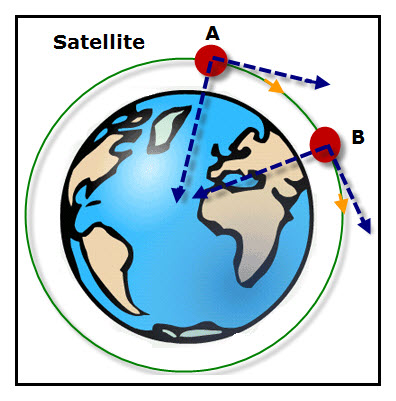
Если бы спутник или МКС не двигались вокруг Земли с громадной скоростью, они бы сразу же упали на поверхность. Эта скорость не ощущается космонавтами из-за принципа относительности.
Гравитационное поле можно компенсировать ускоренным движением лишь в малой области пространства. Если размеры объекта сопоставимы с радиусом Земли, будут заметны эффекты, связанные с неоднородностью гравитационного поля.
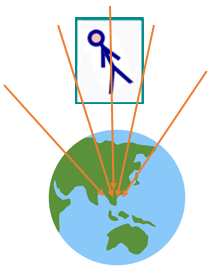
Сила, действующая на пол лифта будет больше чем сила, действующая на потолок из-за их разного удаления от центра Земли. Будет наблюдаться эффективная сила «растягивающая» лифт. Да и направление центростремительной силы в разных частях лифта будет разное что также можно обнаружить. Принцип эквивалентности работает только локально — фактически только для точечного объекта.
Все о чем мы говорили есть следствия классической Ньютоновской механики. Но Эйнштейн своей специальной теорией относительности (СТО) показал, что она не верна при движении со скоростями близкими к скорости света. СТО позволяет исследовать не только движения с постоянной скоростью, но и ускоренные движения. При этом также возникают релятивистские эффекты в виде замедления времени и возникновения горизонта событий. Принцип эквивалентности позволил Эйнштейну применить СТО для анализа гравитационных явлений и выявить аналогичные эффекты для гравитации.
Даже геометрическая интерпретация СТО оказалась полезной и была расширена в итоге в общую теорию относительности (ОТО). Пространство Минковского локально (в окрестности точки) хорошо аппроксимирует искривленное пространство-время общей теории относительности. Можно провести аналогию с тем как геометрия на плоскости хорошо аппроксимирует геометрию на сфере в небольшой окрестности, малой по сравнению с радиусом сферы.
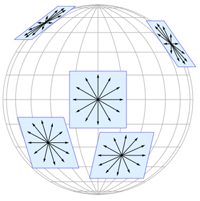


Наземные эксперимены по проверке слабой формы принципа эквивалентности по измерению ускорений различных тел дают относительную точность
Видно, что математика ОТО сложнее математики КМ))
Наборту ускоренно движущейся ракеты свет и вещество «падают » одинаковым ускорением. В поле тяготения же свет «падает» с ускорением в полтора раза бо’льшим вещества.