Гамильтониан. Оператор энергии.

Напомним основные постулаты квантовой механики, связанные с эрмитовыми операторами:

1. Все величины, которые можно экспериментально измерить, в квантовой механике выражаются эрмитовыми операторами (матрицами).
2. Результатом измерения величины, описываемой оператором, может являться только одно из собственных значений данного оператора.
3. Собственные векторы эрмитовых операторов формируют базис по которому можно разложить исходный вектор состояния.
4. Вектор состояния, описывающий систему, после измерения коллапсирует в один из собственных векторов оператора измеряемой величины, причем в тот, который соответствует измеренному собственному значению.
5. Коэффициенты в разложении по базисным векторам исходного вектора состояния есть амплитуды вероятности при измерении обнаружить собственное значение, связанное с данным собственным вектором.

Оператор, связанный с измерением энергии, в квантовой механике называется оператором Гамильтона или Гамильтонианом. Конкретный вид матрицы Гамильтониана зависит от деталей рассматриваемой системы. Если это система с двумя состояниями типа кубита с двумя базисными векторами, то Гамильтониан имеет вид квадратной матрицы 2х2. В общем случае он может быть и бесконечномерной матрицей.

В классической механике энергия частицы складывается из кинетической \( \displaystyle T\) и потенциальной \( \displaystyle V\). Кинетическая энергия  равна:

\( \displaystyle T = \frac{mv^2}{2}= \frac{p^2}{2m}\) где \( \displaystyle p = mv\) — импульс.

Квантовомеханический аналог получается простой заменой числового значения импульса на оператор:

\( \displaystyle \hat{T} = \frac{\hat{p}^{2}}{2m} \)

Сам оператор импульса в квантовомеханическом случае выражается через оператор взятия производной:

\( \displaystyle \hat{p}=-i \frac{d}{dx}\)

Мы получили оператор Гамильтона в координатном базисе:

\( \displaystyle \hat{H} = -\frac{1}{2m}\frac{d^{2}}{dx^2}+V(x) \)

Его собственные векторы также бесконечномерные — это функции от координаты x. Аппроксимируя вторую производную квадратной матрицей и прибавляя дискретизированную функцию потенциала \( \displaystyle V\) получим конечномерную матрицу, аппроксимирующую Гамильтониан:

\( \displaystyle \hat{H}=-\frac{1}{2m(\Delta x)^2}\begin{pmatrix}
-2+V(x_1)&1 &0 &…  \\
1&-2+V(x_2) &1 &…  \\
0&1 &-2+V(x_3) &… \\
…&… &… &… &\\
\end{pmatrix}\)

 

Все что остается — это выбрать конкретный вид функции потенциала и найти на компьютере собственные векторы и собственные значения данной матрицы.

Давайте возьмем квадратичный потенциал \( \displaystyle V = kx^2\), отвечающий линейной силе в классическом случае (пружина, маятник). Система известна как гармонический осциллятор. Найдя собственные значения мы получим, что они отстоят друг от друга на одинаковом расстоянии, причем первый энергетический уровень не нулевой. Квантовый гармонический осциллятор, в отличие от классического, оказывается не может не совершать колебания (иметь нулевую энергию).

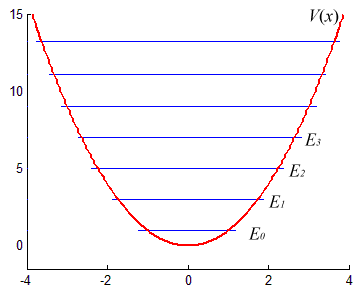
Мы наблюдаем эффект квантования. Измеренная энергия не может принимать любое значение, а только одно из разрешенных, дискретных.

Численные величины собственных значений оператора Гамильтона зависят от вида функции потенциальной энергии. Возьмем, например, второй популярный пример — потенциал в виде прямоугольной ямы.

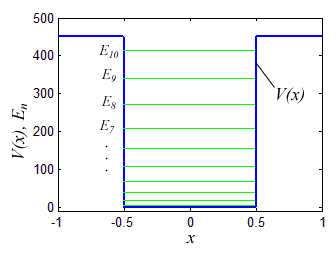
Каждому собственному значению (энергетическому уровню) соответствует собственный вектор — волновая функция в которую перейдет вектор состояния после измерения данного собственного значения (энергии). Несколько собственных функций, соответствующих нескольким первым собственным значениям Гамильтониана с прямоугольным потенциалом приведены на рисунке.

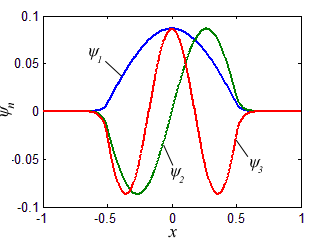
Из рисунка понятно почему квантовомеханический вектор состояния исторически получил название волновой функции. Аналогично можно найти и спектр атома водорода взяв за \( \displaystyle V(x) \) кулоновский потенциал притяжения электрона и протона:

\( \displaystyle V(x) = -\frac{e^2}{4 \pi \epsilon_0 |x|}\)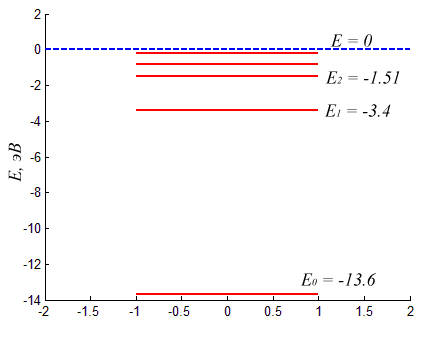

Оператор Гамильтона выделяется среди других эрмитовых операторов тем, что он является генератором эволюции во времени вектора состояния (поэтому он входит в уравнение Шредингера). В связи с этим ряд высказываний касательно времени можно сформулировать используя Гамильтониан. Так утверждение, что величина сохраняется означает ее неизменность с течением времени. На языке оператора Гамильтона данный факт преобразуется в:

Если данный эрмитов оператор коммутирует с Гамильтонианом, то физическая величина, представляемая данным оператором, сохраняется.

То есть, если \( \displaystyle [A,H]=AH-HA=0\), то \( \displaystyle A\) сохраняется.

Тривиальный случай — это закон сохранения энергии, поскольку любой оператор коммутирует сам с собой:

\( \displaystyle [H,H]=0 \Rightarrow\) энергия сохраняется.

Все теперь в телеграм: https://t.me/lightcone_qm